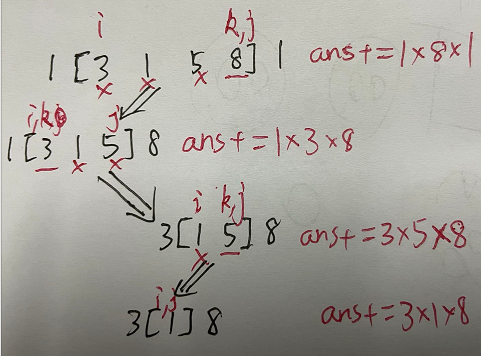01.01[312. Burst Balloons]
传送门
You are given n balloons, indexed from 0 to n - 1. Each balloon is painted with a number on it represented by an array nums. You are asked to burst all the balloons.
If you burst the ith balloon, you will get nums[i - 1] * nums[i] * nums[i + 1] coins. If i - 1 or i + 1 goes out of bounds of the array, then treat it as if there is a balloon with a 1 painted on it.
Return the maximum coins you can collect by bursting the balloons wisely.
Example 1:
1
2
3
4
5
|
Input: nums = [3,1,5,8]
Output: 167
Explanation:
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167
|
Example 2:
1
2
|
Input: nums = [1,5]
Output: 10
|
Constraints:
n == nums.length1 <= n <= 5000 <= nums[i] <= 100
分析:看到题目后再看数组长度限制,就联想到了是不是DP。DP没有很好的想法,先考虑递归吧。这里是不是可以用分治法,怎么用呢?这可以用DP做的,应该有多种相关的不同的计算方法,取最大值。而分治法有个特点是选择一个pivot,那么这里就是这样做的。**值得指出的是:题意说如果要爆掉的那个球左边或右边没有球则它的值视为1,那么在数组首尾添加一个1。**这样的话可以得出下面的图,因为是递归,所以递归树的根(也就是最后爆掉的一个球对应案例1中的8)。递归树的每一个节点对应一次爆球,每次选择不同的pivot,共有n次,因此时间复杂度为O(nlogn),一个二维数组dp[n][n](dp[i][j]:nums[i, …, j]对应的最大值,即$dp[i][j] = \mathop{max}\limits_{k\in[i,j]}(dp[i][k]+dp[k][j])$)空间复杂度为O($n^2$)。
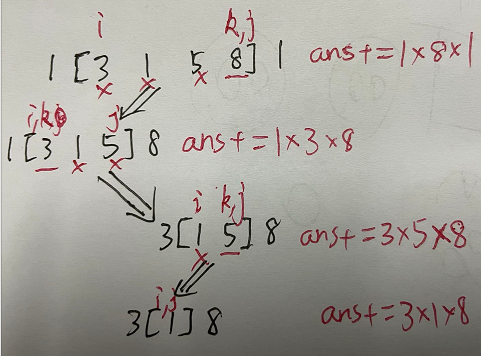
前面说的分治法 是 自上而下的,可以知道的是转化为DP,自下而上计算。
动态规划(DP)三步走:
- DP数组定义
- dp[i][j]:nums[i, …, j]对应的最大值
- 状态转移公式
- $dp[i][j] = 0, i>j, dp[i][i]=nums[i]$
- $dp[i][j] = \mathop{max}\limits_{k\in[i,j]}(dp[i][k]+dp[k][j])$ 具体化=> $dp[i][j] = dp[i][k-1]+dp[k][k]+dp[k+1][j]$
- 讨论k的特殊值,(实际上这里只需要dp数组的初始值都为0,这里就不用讨论了)
- $k=i, dp[i][j] = 0 + nums[i-1]*nums[k]*nums[j+1] + dp[k+1][j]$
- $k=j, dp[i][j] = dp[i][k-1] + nums[i-1]*nums[k]*nums[j+1] + 0$
- 初始值
- 上一步已经写出来了
- $dp[i][j] = 0, i>j, dp[i][i]=nums[i]$
需要强调的是关于 i, j, k遍历的顺序不能反了。把分治法写几个出来看看。这里具体看讨论区的一个解释:
https://leetcode.com/problems/burst-balloons/discuss/733279/DP-Intuitive-explannations-complete-demo-NEVER-confused-with-DP-again
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
i: from len-1 to 0, (direction of i never mind)
j: from i to len-1, (direction of j should start from i)
k: from i to j. (direction of k never mind)
we fill the dp[][] table like:
j,→,→,→,len-1
0 [x,→,→,→,len-1]
↑ [\,x,→,→,len-1]
↑ [\,\,x,→,len-1]
↑ [\,\,\,x,len-1]
i [\,\,\,\,x] direction of k never mind)
or
i [x,\,\,\,\]
↓ [0,x,\,\,\]
↓ [0,←,x,\,\]
↓ [0,←,←,x,\]
len-1 [0,←,←,←,x]
0,←,←,←,j direction of k never mind
using [3,1,5,8] as an example, direction of i from len-1 to 0.
i=3,j=3,k=3: get dp[3][3],
i=2,j=2,k=2: get dp[2][2],
j=3,k=2/3: get dp[2][3] relied on dp[3][3] and dp[2][2]
i=1,j=1,k=1: get dp[1][1]
j=2,k=1/2: get dp[1][2] relied on dp[2][2] and dp[1][1]
j=3,k=1/2/3: get dp[1][3] relied on dp[2][3] and dp[1][1],dp[3][3] and dp[1][2]
…
Maximum Order: using [3,1,5,8] as example.
dp[0][3] = 1*8*1 + dp[0][2] select 8 as the last one / forth
= 1*8*1 + 1*3*8 + dp[1][2] select 3 as the last two / third
= 1*8*1 + 1*3*8 + 3*5*8 + dp[1][1] select 5 as the last three / secon
= 1*8*1 + 1*3*8 + 3*5*8 + 3*1*5 select 1 as the last four / first
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
// 分治法 + 记忆化,time complexity:O(nlogn),自上而下
class Solution {
public:
int maxCoins(vector<int>& nums) {
int n = nums.size();
nums.resize(n+2, 1); // 重置数组大小为n+2,新添加的元素用1填充
for(int i=0; i<=n; i++) {
swap(nums[n-i], nums[n-i+1]);
}
// 此时,案例1的数组元素为[1, 3, 1, 5, 8, 1]
n += 2;
vector<vector<int>>dp(n, vector<int>(n-1, -1));
return divideConquer(nums, 1, n-2, n, dp);
}
int divideConquer(vector<int>& nums, int i, int j, const int n, vector<vector<int>>& dp) {
if(dp[i][j] != -1) return dp[i][j];
if(i > j) return dp[i][j] = 0;
if(i == j) {
// 只有一个元素
int temp = nums[i];
if(i-1 >= 0) temp *= nums[i-1];
if(j+1 < n) temp *= nums[j+1];
return dp[i][j] = temp;
}
int ans = 0; // 存储结果
for (int k=i; k<=j; k++) {
int temp = nums[k];
if(j+1 < n) temp *= nums[j+1];
if(i-1 >= 0) temp *= nums[i-1];
temp += divideConquer(nums, i, k-1, n, dp)
+ divideConquer(nums, k+1, j, n, dp);
if (ans < temp) ans = temp;
}
return dp[i][j] = ans;
}
};
// DP,自下而上。时间复杂度O(n^2),空间复杂度O(n^2)。才打败35%?别人都咋写的,我在想想?双循环?不可能吧?
class Solution {
public:
int maxCoins(vector<int>& nums) {
int n = nums.size();
nums.resize(n+2, 1);
for(int i=0; i<=n; i++) {
swap(nums[n-i], nums[n-i+1]);
}
n += 2;
vector<vector<int>>dp(n, vector<int>(n, 0));//初始化为0
for(int i=n-2; i>=1; i--) {
for (int j=i; j<n-1; j++) {
for (int k=i; k<=j; k++) {
int temp = 0;
temp += dp[i][k-1] + nums[i-1] * nums[k] * nums[j+1] + dp[k+1][j]; // i=j=k, temp = nums[k-1]*nums[k]*nums[k+1] 即 temp = dp[k][k]
if(dp[i][j] < temp) {
dp[i][j] = temp;
}
}
}
}
return dp[1][n-2];
}
};
|
01.02[\1010. Pairs of Songs With Total Durations Divisible by 60]
传送门
You are given a list of songs where the ith song has a duration of time[i] seconds.
Return the number of pairs of songs for which their total duration in seconds is divisible by 60. Formally, we want the number of indices i, j such that i < j with (time[i] + time[j]) % 60 == 0.
Example 1:
1
2
3
4
5
6
|
Input: time = [30,20,150,100,40]
Output: 3
Explanation: Three pairs have a total duration divisible by 60:
(time[0] = 30, time[2] = 150): total duration 180
(time[1] = 20, time[3] = 100): total duration 120
(time[1] = 20, time[4] = 40): total duration 60
|
Example 2:
1
2
3
|
Input: time = [60,60,60]
Output: 3
Explanation: All three pairs have a total duration of 120, which is divisible by 60.
|
Constraints:
1 <= time.length <= 6 * 1041 <= time[i] <= 500
分析:笨办法:双循环暴力查找,明显超时。 有点像两数之和,但这里找出另外一个数的表达式 y = (60 - x % 60) % 60,对60取模后计数统计。因为有要求i<j,这里边顺序访问 边计数(ans+=mp[y], mp[x%60] ++)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
// 时间复杂度O(n),空间复杂度O(n)
class Solution {
public:
int numPairsDivisibleBy60(vector<int>& time) {
int mp[60] = {}; // 这样比map<int, int>mp; 快一点,但是也只打败了27%(时间)?
int ans = 0;
for(auto x: time) {
int y = (60 - x % 60) % 60;
ans += mp[y];
mp[x % 60] ++;
}
return ans;
}
};
|
大概看了下讨论区里的做法,一种是上面这样,另外还有一个先计算mp[x%60]频次,然后计算结果(但是不明白的是为什么特例0 和 30的频次计算公式是n*(n-1) / 2 ,通过样例确实可以说明可用,但是证明呢??这个还没看明白)。。
先贴出来, 哪天明白了再补上
链接:https://leetcode.com/problems/pairs-of-songs-with-total-durations-divisible-by-60/discuss/964469/C%2B%2B-Linear-Solution-Explained-~100-Time-~95-Space
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public:
int numPairsDivisibleBy60(vector<int>& time) {
// support variables
int freqs[60] = {}, res = 0;
// populating freqs
for (int t: time) freqs[t % 60]++;
// computing the number of matches for most pairs
for (int i = 1; i < 30; i++) res += freqs[i] * freqs[60 - i];
// special cases - 0s and 30s
res += freqs[0] * (freqs[0] - 1) / 2 + freqs[30] * (freqs[30] - 1) / 2;
return res;
}
};
|
01.03[\997. Find the Town Judge]
传送门
In a town, there are n people labeled from 1 to n. There is a rumor that one of these people is secretly the town judge.
If the town judge exists, then:
- The town judge trusts nobody.
- Everybody (except for the town judge) trusts the town judge.
- There is exactly one person that satisfies properties 1 and 2.
You are given an array trust where trust[i] = [ai, bi] representing that the person labeled ai trusts the person labeled bi.
Return the label of the town judge if the town judge exists and can be identified, or return -1 otherwise.
Example 1:
1
2
|
Input: n = 2, trust = [[1,2]]
Output: 2
|
Example 2:
1
2
|
Input: n = 3, trust = [[1,3],[2,3]]
Output: 3
|
Example 3:
1
2
|
Input: n = 3, trust = [[1,3],[2,3],[3,1]]
Output: -1
|
Constraints:
1 <= n <= 10000 <= trust.length <= 104trust[i].length == 2- All the pairs of
trust are unique.
ai != bi1 <= ai, bi <= n
分析:满足题意的条件:1)只有一个镇判官;2)镇判官 不信任任何人;3)所有人(除了真判官自己)都信任镇判官。 给定二维数组trust,其中$a_i$信任$b_i$。 统计每个节点的入度和出度,只要入度为n-1且出度为0的节点则为所求。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
// 时间复杂度O(max(trust.length, n)),空间复杂度O(n)
class Solution {
public:
int findJudge(int n, vector<vector<int>>& trust) {
if(trust.empty() && n==1) return 1;
// vector<int> inDegree(n), outDegree(n) //统计入度和出度
vector<int> inDegree(n);
for (auto elem: trust) {
// outDegree[elem[0]-1]++;
inDegree[elem[0]-1]--;
inDegree[elem[1]-1]++;
}
int ans = -1;
for(int i=0; i<n; i++) {
if(inDegree[i] == n-1) { // 入度与出度之和 = n-1即为所求
ans = i+1;
}
}
return ans;
}
};
|
01.04[\1009. Complement of Base 10 Integer]
传送门
The complement of an integer is the integer you get when you flip all the 0’s to 1’s and all the 1’s to 0’s in its binary representation.
- For example, The integer
5 is "101" in binary and its complement is "010" which is the integer 2.
Given an integer n, return its complement.
Example 1:
1
2
3
|
Input: n = 5
Output: 2
Explanation: 5 is "101" in binary, with complement "010" in binary, which is 2 in base-10.
|
Example 2:
1
2
3
|
Input: n = 7
Output: 0
Explanation: 7 is "111" in binary, with complement "000" in binary, which is 0 in base-10.
|
Example 3:
1
2
3
|
Input: n = 10
Output: 5
Explanation: 10 is "1010" in binary, with complement "0101" in binary, which is 5 in base-10.
|
Constraints:
Note: This question is the same as 476: https://leetcode.com/problems/number-complement/
分析:
101 ^ 111 = 010 = 2
1
2
3
4
5
6
7
8
9
10
|
class Solution {
public:
int bitwiseComplement(int n) {
int num = 1;
while (num < n) {
num = (num << 1) | 1;
}
return num ^ n;
}
};
|
01.05[\131. Palindrome Partitioning]
传送门
Given a string s, partition s such that every substring of the partition is a palindrome. Return all possible palindrome partitioning of s.
A palindrome string is a string that reads the same backward as forward.
Example 1:
1
2
|
Input: s = "aab"
Output: [["a","a","b"],["aa","b"]]
|
Example 2:
1
2
|
Input: s = "a"
Output: [["a"]]
|
Constraints:
1 <= s.length <= 16s contains only lowercase English letters.
分析:输出字符串s所有可能的回文子串划分。 因为是所有的,所以想到用递归+回溯。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
// 递归+回溯 O(n^2)
class Solution {
public:
vector<vector<string>> partition(string s) {
vector<vector<string>> res;
vector<string>strArr;
dfs(s, strArr, res, 0);
return res;
}
// index表示 子串第一个字符在母串s对应的位置
void dfs(const string &s, vector<string>& strArr, vector<vector<string>>& res, int i) {
if (i == s.size()) {
res.push_back(strArr);
return;
}
// 枚举子串的最后一个位置
for (int j=i; j<s.size(); j++) {
if (isPalindrome(s, i, j)) { // s[index, ..., i] 是回文串
strArr.push_back(s.substr(i, j-i+1));
dfs(s, strArr, res, j+1);
strArr.pop_back(); // 回溯
}
}
}
// 判断子串s[i, ..., j] 是否为回文串
bool isPalindrome(const string &s, int i, int j) {
while (i <= j) {
if (s[i++] != s[j--]) return false;
}
return true;
}
};
|
01.06[\1094. Car Pooling]
传送门
There is a car with capacity empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer capacity and an array trips where trip[i] = [numPassengersi, fromi, toi] indicates that the ith trip has numPassengersi passengers and the locations to pick them up and drop them off are fromi and toi respectively. The locations are given as the number of kilometers due east from the car’s initial location.
Return true if it is possible to pick up and drop off all passengers for all the given trips, or false otherwise.
Example 1:
1
2
|
Input: trips = [[2,1,5],[3,3,7]], capacity = 4
Output: false
|
Example 2:
1
2
|
Input: trips = [[2,1,5],[3,3,7]], capacity = 5
Output: true
|
Constraints:
1 <= trips.length <= 1000trips[i].length == 31 <= numPassengersi <= 1000 <= fromi < toi <= 10001 <= capacity <= 105
分析:记录在每一战 上下车的人数,枚举每一站, 判断当前剩余的容量capacity是否能够容纳stops[i]个人
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public:
bool carPooling(vector<vector<int>>& trips, int capacity) {
int stops[1001] = {0};
for (auto trip: trips) {
stops[trip[1]] += trip[0]; // trip[0]个人上车
stops[trip[2]] -= trip[0]; // 下车
}
for (int i=0; i<1001 && capacity>=0; i++) {
capacity -= stops[i];
}
return capacity >= 0;
}
};
|
01.07[\382. Linked List Random Node]
传送门
Given a singly linked list, return a random node’s value from the linked list. Each node must have the same probability of being chosen.
Implement the Solution class:
Solution(ListNode head) Initializes the object with the integer array nums.int getRandom() Chooses a node randomly from the list and returns its value. All the nodes of the list should be equally likely to be choosen.
Example 1:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
Input
["Solution", "getRandom", "getRandom", "getRandom", "getRandom", "getRandom"]
[[[1, 2, 3]], [], [], [], [], []]
Output
[null, 1, 3, 2, 2, 3]
Explanation
Solution solution = new Solution([1, 2, 3]);
solution.getRandom(); // return 1
solution.getRandom(); // return 3
solution.getRandom(); // return 2
solution.getRandom(); // return 2
solution.getRandom(); // return 3
// getRandom() should return either 1, 2, or 3 randomly. Each element should have equal probability of returning.
|
Constraints:
- The number of nodes in the linked list will be in the range
[1, 104].
-104 <= Node.val <= 104- At most
104 calls will be made to getRandom.
Follow up:
- What if the linked list is extremely large and its length is unknown to you?
- Could you solve this efficiently without using extra space?
分析:follow up中 要求链表极大且不知道长度,要求不使用额外空间。
转换为vector会占用额外的空间。
那么可以预设一个长度len 表示链表长度,随机选择一个节点,然后遍历找到该节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
// 预设一个链表长度len
class Solution {
public:
ListNode *Head = nullptr;
int len = 0;
Solution(ListNode* head) {
this->Head = head;
while (head != nullptr) {
this->len ++;
head = head->next;
}
}
int getRandom() {
int mod = rand() % this->len;
ListNode* pHead = this->Head;
while (mod) {//从头遍历链表找到该节点
pHead = pHead->next;
mod --;
}
return pHead->val;
}
};
class Solution {
public:
ListNode *Head = nullptr;
Solution(ListNode* head) {
this->Head = head;
}
int getRandom() {
int ans, mod = 1;
ListNode *pHead = this->Head;
while (pHead != nullptr) {
if(rand() % mod == 0) ans = pHead->val;
mod ++;
pHead = pHead->next;
}
return ans;
}
};
|
01.08[\1463. Cherry Pickup II]
传送门
You are given a rows x cols matrix grid representing a field of cherries where grid[i][j] represents the number of cherries that you can collect from the (i, j) cell.
You have two robots that can collect cherries for you:
- Robot #1 is located at the top-left corner
(0, 0), and
- Robot #2 is located at the top-right corner
(0, cols - 1).
Return the maximum number of cherries collection using both robots by following the rules below:
- From a cell
(i, j), robots can move to cell (i + 1, j - 1), (i + 1, j), or (i + 1, j + 1).
- When any robot passes through a cell, It picks up all cherries, and the cell becomes an empty cell.
- When both robots stay in the same cell, only one takes the cherries.
- Both robots cannot move outside of the grid at any moment.
- Both robots should reach the bottom row in
grid.
Example 1:
1
2
3
4
5
6
|
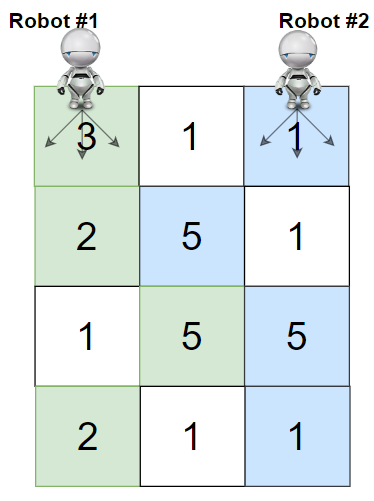
Input: grid = [[3,1,1],[2,5,1],[1,5,5],[2,1,1]]
Output: 24
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (3 + 2 + 5 + 2) = 12.
Cherries taken by Robot #2, (1 + 5 + 5 + 1) = 12.
Total of cherries: 12 + 12 = 24.
|
Example 2:
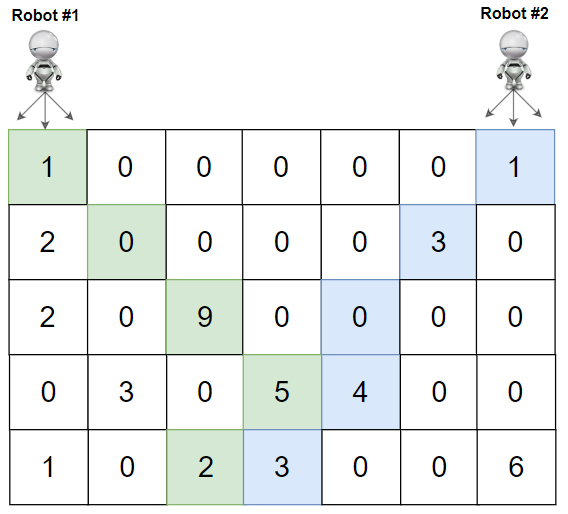
1
2
3
4
5
6
|
Input: grid = [[1,0,0,0,0,0,1],[2,0,0,0,0,3,0],[2,0,9,0,0,0,0],[0,3,0,5,4,0,0],[1,0,2,3,0,0,6]]
Output: 28
Explanation: Path of robot #1 and #2 are described in color green and blue respectively.
Cherries taken by Robot #1, (1 + 9 + 5 + 2) = 17.
Cherries taken by Robot #2, (1 + 3 + 4 + 3) = 11.
Total of cherries: 17 + 11 = 28.
|
Constraints:
rows == grid.lengthcols == grid[i].length2 <= rows, cols <= 700 <= grid[i][j] <= 100
分析:这里robot1和robot2需要同时移动, 因为不同时移动的话,先者会影响后者的移动轨迹。
dp(row, col1, col2) 表示 robot1在(row, col1), robot2在(row, col2) 时的收集的cherries的最大值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
// 自顶向下 dfs+记忆化 时间复杂度O(n m^2) 空间复杂度O(n m^2)
class Solution {
public:
int cherryPickup(vector<vector<int>>& grid) {
int n = grid.size();
int m = grid[0].size();
vector<vector<vector<int>>> dp(n, vector<vector<int>>(m, vector<int>(m, -1)));
return dfs(0, 0, m-1, grid, dp);
}
private:
int dfs(int row, int col1, int col2, vector<vector<int>>&grid, vector<vector<vector<int>>> &dp) {
// 越界
if (col1 < 0 || col1 >= grid[0].size() || col2 < 0 || col2 >= grid[0].size()) {
return 0;
}
if (dp[row][col1][col2] != -1) return dp[row][col1][col2];
// 当前的一步收集的cherry
int res = 0;
res += grid[row][col1];
if (col1 != col2) res += grid[row][col2];
// 状态转移
if (row != grid.size() - 1) {
int maxCherries = 0;
for (int i = col1 - 1; i <= col1 + 1; i++) {
for (int j = col2 - 1; j <= col2 + 1; j++) {
maxCherries = max(maxCherries, dfs(row+1, i, j, grid, dp));
}
}
res += maxCherries;
}
dp[row][col1][col2] = res;
return res;
}
};
// 自底向上, 时间复杂度 空间复杂度与 自顶向下相同。
class Solution {
public:
int cherryPickup(vector<vector<int>>& grid) {
int n = grid.size();
int m = grid[0].size();
vector<vector<vector<int>>> dp(n, vector<vector<int>>(m, vector<int>(m, 0)));
for (int row=n-1; row>=0; row--) {
for (int col1=0; col1<m; col1++) {
for (int col2=0; col2<m; col2++) {
int res = 0;
res += grid[row][col1];
if(col1 != col2) {
res += grid[row][col2];
}
if(row != n-1) {
int maxCherries = 0;
for (int i=col1-1; i<=col1+1; i++) {
for (int j=col2-1; j<=col2+1; j++) {
if (i<0 || i>=m || j<0 || j>=m) continue;
maxCherries = max(maxCherries, dp[row+1][i][j]);
}
}
res += maxCherries;
}
dp[row][col1][col2] = res;
}
}
}
return dp[0][0][m-1];
}
};
|
01.09.[\1041. Robot Bounded In Circle]
传送门
On an infinite plane, a robot initially stands at (0, 0) and faces north. The robot can receive one of three instructions:
"G": go straight 1 unit;"L": turn 90 degrees to the left;"R": turn 90 degrees to the right.
The robot performs the instructions given in order, and repeats them forever.
Return true if and only if there exists a circle in the plane such that the robot never leaves the circle.
Example 1:
1
2
3
4
|
Input: instructions = "GGLLGG"
Output: true
Explanation: The robot moves from (0,0) to (0,2), turns 180 degrees, and then returns to (0,0).
When repeating these instructions, the robot remains in the circle of radius 2 centered at the origin.
|
Example 2:
1
2
3
|
Input: instructions = "GG"
Output: false
Explanation: The robot moves north indefinitely.
|
Example 3:
1
2
3
|
Input: instructions = "GL"
Output: true
Explanation: The robot moves from (0, 0) -> (0, 1) -> (-1, 1) -> (-1, 0) -> (0, 0) -> ...
|
Constraints:
1 <= instructions.length <= 100instructions[i] is 'G', 'L' or, 'R'.
分析:判断行进方向和当前位置,具体见代码注释
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
// 时间复杂度O(n), 空间复杂度O(1)
class Solution {
public:
bool isRobotBounded(string instructions) {
// 在初始位置默认是向右走的,所以dir[1][0]=0, dir[1][1]=1; 前进方向:右 上 左 下
int dir[4][2] = {0, 1, -1, 0, 0, -1, 1, 0};
int direction = 0, x = 0, y = 0; //(x, y)表示当前位置, direction表示当前位置的方向
for (auto ch: instructions) {
if (ch == 'L') { // 左转90°,朝上走
direction = (direction + 1) % 4;
} else if(ch == 'R') { // 右转90°,朝下走
direction = (direction + 3) % 4;
} else { // 按照当前方向前进
x += dir[direction][0];
y += dir[direction][1];
}
}
// 回到原点(0, 0) 或者 方向不朝北(原因是无限重复instructions这条指令)
return (x == 0 && y == 0) || direction > 0;
}
};
|
01.10[\67. Add Binary]
传送门
分析:二进制加法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
string addBinary(string a, string b) {
int lenA = a.size();
int lenB = b.size();
string res = "";
int carry=0, i, j;
for (i=lenA-1, j=lenB-1; i>=0 && j>=0; i--, j--) {
int temp = (carry + a[i]-'0' + b[j]-'0') % 2;
res += (temp+'0');
carry = (carry + a[i]-'0' + b[j]-'0') / 2;
}
while (i>=0) {
int temp = (carry + a[i]-'0') % 2;
res += (temp+'0');
carry = (carry + a[i--]-'0') / 2;
}
while (j>=0) {
int temp = (carry + b[j]-'0') % 2;
res += (temp+'0');
carry = (carry + b[j--]-'0') / 2;
}
if(carry) res += char(carry+'0');
reverse(res.begin(), res.end());
return res;
}
};
|
01.11[\1022. Sum of Root To Leaf Binary Numbers]
传送门
分析:先序遍历。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int sumRootToLeaf(TreeNode* root) {
int res = 0;
vector<char>s;
dfs(root, res, s);
return res;
}
void dfs(TreeNode* root, int& res, vector<char> s) {
if(root == nullptr) return;
s.push_back(root->val + '0');
if(root->left == nullptr && root->right == nullptr) {
res += binary2Ten(s);
s.pop_back();
return;
}
dfs(root->left, res, s);
dfs(root->right, res, s);
}
inline int binary2Ten(vector<char> s) {
int num = 0;
for(auto ch: s) {
num = num * 2 + (ch - '0');
}
return num;
}
};
|
01.12[\701. Insert into a Binary Search Tree]
传送门
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
// 迭代。时间复杂度O(logn) 空间复杂度O(1) beats 35% / 50%
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (root == nullptr) return new TreeNode(val);
TreeNode* cur = root, *pre = nullptr;
while (cur != nullptr) {
pre = cur;
if (cur->val > val) cur = cur->left;
else cur = cur->right;
}
if (pre->val < val) pre->right = new TreeNode(val);
else pre->left = new TreeNode(val);
return root;
}
};
// 堆栈出错!! 递归,时间和空间复杂度O(logn)
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (root == nullptr) return new TreeNode(val);
if (root->val < val) root->right = insertIntoBST(root, val);
else root->left = insertIntoBST(root, val);
return root;
}
};
|
01.13[\452. Minimum Number of Arrows to Burst Balloons]
传送门
分析:位于x的一支箭可以打爆任何一个直径包含x的气球。只知道x轴,将其看着做是一条线段。按照points数组第二个元素排序,将第二个元素point[i][1]作为额外一支箭打爆气球的位置,ans++。因为前面做了排序,所以maxn>=point[i][0]的气球则不需要额外的箭。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
public:
// 按第二个元素排序
static inline bool cmp(vector<int> &a, vector<int>&b) {
return a[1] < b[1];
}
int findMinArrowShots(vector<vector<int>>& points) {
sort(points.begin(), points.end(), cmp);
int maxn = points[0][1], ans=1;
for (int i=0; i<points.size(); i++) {
if (maxn < points[i][0]) {
maxn = points[i][1];
ans ++;
}
}
return ans;
}
};
|
01.14[\8. String to Integer (atoi)]
传送门
01.15[\1345. Jump Game IV]
传送门
01.16[\849. Maximize Distance to Closest Person]
传送门
分析:prev记录上一个seats[i] = 1的位置,i为当前位置,next记录下一个seats[i]=1的位置。
ans = max(ans, min(left, right))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public:
int maxDistToClosest(vector<int>& seats) {
int prev = -1;
int ans = 0, n = seats.size();
for (int i=0; i<n; i++) {
if (seats[i] == 1) {
prev = i;
} else {
int next = i;
while (next < n && seats[next] == 0) {
next ++;
}
int left = (prev == -1) ? n : (i - prev);
int right = (next == n) ? n : (next - i);
ans = max(ans, min(left, right));
}
}
return ans;
}
};
|
01.17[\290. Word Pattern]
传送门
分析:非空字符串s的一个词符合pattern的一个字母存在双射(bijection):完全匹配。
使用两个map 与index做映射。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
// 时间复杂度O(m) m为s的单词数,空间复杂度O(m)
class Solution {
public:
bool wordPattern(string pattern, string s) {
unordered_map<char, int> pattern2index;
unordered_map<string, int> word2index;
int i=0, len = pattern.size();
istringstream input(s);
string word;
while (input >> word) { // 从流中输入
if (i == len || pattern2index[pattern[i]] != word2index[word]) {
// pattern已经遍历完了 或 pattern[i]与word不能形成bijection
return false;
}
pattern2index[pattern[i]] = word2index[word] = i+1;// +1的原因是因为map的value默认为0,所以最小的value应为1,避免出错
i++;
}
return i == len; // 恰好形成bijection
}
};
|
01.18[\605. Can Place Flowers]
传送门
分析:从左至右在每个能放flower的位置(其左右两边是0或者是边界)放flower(即 置flower[i]=1)。为了方便统一处理,数组首尾添加一个0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
// 时间复杂度O(n) 空间复杂度O(1)
class Solution {
public:
bool canPlaceFlowers(vector<int>& flowerbed, int n) {
flowerbed.insert(flowerbed.begin(), 0);
flowerbed.push_back(0); // 方便统一处理
int len = flowerbed.size();
for (int i=1; i<len-1 && n>0; i++) {// n>0判断可以减少循环执行次数
if (flowerbed[i-1] == 0 && flowerbed[i] == 0 && flowerbed[i+1] == 0) {
flowerbed[i] = 1;
n--;
}
}
return n==0;
}
};
|
01.19[]
01.20[\875. Koko Eating Bananas]
传送门
分析:暴力查找,通过枚举Koko吃香蕉的速度speed(递增),计算实际耗时rh并与h比较,直到speed满足 实际耗时rh<=h。 但是这样的时间复杂度是O(nm),n是piles数组的长度,m是枚举speed的次数。当piles数组元素都很大时,一定会超时。
进一步分析,递增枚举,直到一个符合条件的rh。其实这样可以转化为二分法。枚举的speed前面部分都不符合题意,只有临界值 rh* = h以后的speed是符合题意的(即rh<=h)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public:
int minEatingSpeed(vector<int>& piles, int h) {
int left = 1, right = *max_element(piles.begin(), piles.end());
int ans;
while (left < right) {
int mid = left + ((right - left) >> 1);
int hourSpent = 0;
for (auto x: piles) {
hourSpent += (x / mid + (x % mid != 0));
}
if (hourSpent <= h) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
};
|
01.21[\134. Gas Station]
传送门
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
// 时间复杂度O(n)
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
// sum 表示全局和,tank表示当前tank的剩余量
int sum = 0, tank = 0, start = 0, n = gas.size();
for (int i=0; i<n; i++) {
sum += gas[i] - cost[i];
tank += gas[i] - cost[i];
if (tank < 0) {
tank = 0;
start = i + 1;
}
// cout << start << " " << sum << endl;
}
return sum < 0 ? -1 : start;
}
};
|
01.22[\1510. Stone Game IV]
分析:在这道题中分为先后手。而一个关键点就是给出的n对应的结果是确定的。即 先手dp[i] = true时,后手dp[i-k] = false。而k是一个可得平方根的数。 开始写复杂了。。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
|
// 时间复杂度 O(n * sqrt(n)) 空间复杂度O(n)
class Solution {
public:
bool winnerSquareGame(int n) {
vector<bool> dp(n+1, false);
for (int i=1; i<=n; i++) {
for (int j=1; j*j<=i; j++) {
if (dp[i - (j * j)] == false) {
/// 先后走完第一步的状态是false, 即先手胜
dp[i] = true;
break;
}
}
}
return dp[n];
}
};
// WA! 样例: 99
class Solution {
public:
bool winnerSquareGame(int n) {
vector<bool> dp(n+1, false);
int i = 1;
while (i * i <= n) {
dp[i*i] = true;
i++;
}
if ((i-1) * (i-1) == n) { // 可以开方根的数
return true;
}
for (int i=2; i<=n; i++) {
int num = i, sqrtedNum = int(sqrt(i));
if (isSquare(num)) continue;
int ppreSquare = (sqrtedNum - 1) * (sqrtedNum - 1);
// cout << "num = " << num << endl;
for (int j=ppreSquare; j<i; j++) {
int minx = min(j, num-j);
int maxx = max(j, num-j);
int delta = num - maxx, delta2 = num - minx;
// cout << minx << " " << maxx << " delta=" << delta << endl;
if (minx != maxx && ((isSquare(delta) && !dp[maxx])
|| (isSquare(delta2) && !dp[minx])) ) {
// cout << minx << " " << maxx << endl;
// 先手走完第一步的状态为F 即先手获胜,但可能存在dp[2]=false而dp[1]=true的情况,所以需要minx!=maxx
// 先手走的第一步必须满足delta是可开放根的(不需要判断后手,因为这时候得到的一个状态已经是确定的)
// 因为给定的一个数n其结果是确定的,所以可以保存<n的结果状态以便复用
dp[num] = true;
break;
}
}
}
return dp[n];
}
bool isSquare(int n) {
return n && int(sqrt(n)) * int(sqrt(n)) == n;
}
};
|
01.23[\1291. Sequential Digits]
传送门
TODO:现实中数字可能没有上界。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public:
vector<int> sequentialDigits(int low, int high) {
queue<int> q{{1,2,3,4,5,6,7,8,9}};
vector<int> ans;
while (!q.empty()) {
int qfront = q.front();
q.pop();
if (qfront > high) { // 超出范围high
break;
}
if (qfront >= low && qfront <= high) {
ans.push_back(qfront);
}
int num = qfront % 10;
int next = qfront * 10 + (num + 1); // 下一个数
if (num < 9) q.push(next); // 加入队列
}
return ans;
}
};
|
01.24[\520. Detect Capital]
传送门
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public:
bool detectCapitalUse(string word) {
int numUpper = 0;
for (auto ch: word) {
if (isupper(ch)) numUpper++;
}
return numUpper==0
|| numUpper == word.size()
|| numUpper==1 && isupper(word[0]);
}
};
|
01.25[\941. Valid Mountain Array]
传送门
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public:
bool validMountainArray(vector<int>& arr) {
if (arr.size() < 3) return false;
int i = 1, len = arr.size();
while (i < len && arr[i-1] < arr[i]) {
i++;
}
if (i == 1 || i == len) return false;
while (i < len && arr[i-1] > arr[i]) {
i++;
}
return i == len;
}
};
|
01.26[\1305. All Elements in Two Binary Search Trees]
传送门
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
// O(m+n) / O(m+n)
class Solution {
public:
vector<int> getAllElements(TreeNode* root1, TreeNode* root2) {
stack<TreeNode*> stack1, stack2;
vector<int> res;
while (root1 || root2 || !stack1.empty() || !stack2.empty()) {
while (root1) {
stack1.push(root1);
root1 = root1->left;
}
while (root2) {
stack2.push(root2);
root2 = root2->left;
}
if (stack2.empty() || (!stack1.empty() && stack1.top()->val <= stack2.top()->val)) {
root1 = stack1.top();
stack1.pop();
res.push_back(root1->val);
root1 = root1->right;
} else {
root2 = stack2.top();
stack2.pop();
res.push_back(root2->val);
root2 = root2->right;
}
}
return res;
}
};
|