精选高频面试题
-
合并有序链表
-
反转链表
-
单例模式
-
简单工厂模式
-
快速排序
-
归并排序
-
实现一个堆排序
-
设计LRU缓存
-
重排链表
-
奇偶链表
-
写三个线程交替打印ABC
-
Top K问题
-
使用最大最小堆。 求最大的数用 最小堆,求最小的数用 最大堆(以寻找第K大的元素为例)
-
1
2
3
4
5
6
7
8
9
10
|
struct Node {
int value;
int idx;
Node (int v, int i): value(v), idx(i) {}
friend bool operator < (const struct Node &n1, const struct Node &n2) ;
};
inline bool operator < (const struct Node &n1, const struct Node &n2) {
return n1.value < n2.value;
}
priority_queue<Node> pq; // 此时pq为最大堆
|
-
Quick Select算法。 类似快排的思路,根据pivot划分数组
- 首先选取一个枢轴,然后将数组中小于该枢轴的数放到左边,大于该枢轴的数放到右边。
此时,如果左边的数组中的元素个数大于等于K,则第K大的数肯定在左边数组中,继续对左边数组
执行相同操作;
如果左边的数组元素个数等于K-1,则第K大的数就是pivot;
如果左边的数组元素个数小于K,则第K大的数肯定在右边数组中,对右边数组执行相同操作
- 这个算法与快排最大的区别是,每次划分后**只处理左半边或者右半边**,而快排在划分后对左右半边都继续排序
-
使用排序方法,排序后寻找Top K元素
-
使用选择排序的思想,对前K个元素部分排序
-
将100000个数分成m组,每组寻找Top K个数,得到m x K个数,在这m x K个数里面找到Top K个数
-
布隆过滤器原理与优点
LeetCode经典题型
算法思想
双指针
\1. Two Sum —— Easy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
vector<pair<int, int>> v;
for (int i=0; i<nums.size(); i++) {
v.push_back({nums[i], i});
}
std::sort(v.begin(), v.end());
int l = 0, r = nums.size()-1;
vector<int> res;
while (l < r) {
int sum = v[l].first + v[r].first;
if(sum == target) {
res.push_back(v[l].second);
res.push_back(v[r].second);
break;
}
else if(sum < target) l++;
else r--;
}
return res;
}
};
|
\633. Sum of Square Numbers —— Medium
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public:
bool judgeSquareSum(int c) {
long a = 0, b = sqrt(c);
while (a <= b) {
long num = a * a + b * b;
if(num == c) return true;
else if (num < c) a++;
else b--;
}
return false;
}
};
|
\345. Reverse Vowels of a String
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public:
string reverseVowels(string s) {
string vowels = "aeiouAEIOU";
int i = 0, j = s.size()-1;
while (i < j) {
if(vowels.find(s[i]) == -1) {
i++;
continue;
}
if(vowels.find(s[j]) == -1) {
j--;
continue;
}
swap(s[i], s[j]);
i++, j--;
}
return s;
}
};
|
\680. Valid Palindrome II
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
public:
bool validPalindrome(string s) {
for (int i=0, j=s.size()-1; i<j; i++, j--) {
if(s[i] != s[j]) {
return isPalindrome(s, i+1, j) || isPalindrome(s, i, j-1);
}
}
return true;
}
bool isPalindrome(string &s, int i, int j) {
while (i < j && s[i] == s[j]) {
i++, j--;
}
return i >= j;
}
};
|
\88. Merge Sorted Array (Easy)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int i = m-1, j = n-1, k = m+n-1;
while (j >= 0) {
if (i < 0) {
nums1[k--] = nums2[j--];
} else if(nums1[i] < nums2[j]) {
nums1[k--] = nums2[j--];
} else {
nums1[k--] = nums1[i--];
}
}
}
};
|
\141. Linked List Cycle (Easy)
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public:
bool hasCycle(ListNode *head) {
ListNode *fast=head, *slow=head;
while (fast && fast->next) {
fast = fast->next->next;
slow = slow->next;
if (slow == fast) return true;
}
return false;
}
};
|
\524. Longest Word in Dictionary through Deleting (Medium)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public:
string findLongestWord(string s, vector<string>& dictionary) {
string res = "";
for (string &t: dictionary) {
int l1 = res.size(), l2 = t.size();
if(l1 > l2 || (l1 == l2 && res.compare(t) < 0)) { //当前字符串t的长度没有l1长 或者 长度相同但字典序更大
continue;
}
if(isSubstr(s, t)) res = t; // 有更长的子串t
}
return res;
}
bool isSubstr(string &s, string &t) {
int i=0, j=0;
while (i < s.size()) {
if(s[i] == t[j]) j++;
i++;
}
return j == t.size();
}
};
|
排序
贪心思想
\455. Assign Cookies (Easy)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public:
int findContentChildren(vector<int>& g, vector<int>& s) {
std::sort(g.begin(), g.end());
std::sort(s.begin(), s.end());
int i=0, j=0;
while (i < g.size() && j < s.size()) {
if(g[i] <= s[j]) i++;
j++;
}
return i;
}
};
|
二分查找
\69. Sqrt(x) —— Easy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public:
int mySqrt(int x) {
if(x<=1) return x;
int low = 1, high = x;
while (low <= high) { /// 退出循环时,high 总比 low 小1
int mid = low + (high - low) / 2;
int sqrt = x / mid;
if (sqrt == mid) return mid;
else if(sqrt < mid) high = mid - 1;
else low = mid + 1;
}
return high;
}
};
|
\744. Find Smallest Letter Greater Than Target —— Easy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public:
char nextGreatestLetter(vector<char>& letters, char target) {
int l = 0, r = letters.size()-1;
while (l <= r) {
int mid = l + (r - l) / 2;
char c = letters[mid];
if (c <= target) l = mid+1;
else r = mid-1;
}
return l < letters.size() ? letters[l] : letters[0];
}
};
class Solution {
public:
char nextGreatestLetter(vector<char>& letters, char target) {
auto pos = upper_bound(letters.begin(), letters.end(), target); /// 查找 >target 的第一个位置,返回对应的迭代器
return pos == letters.end() ? letters[0] : *pos;
}
};
|
\540. Single Element in a Sorted Array —— Medium
分析:返回出现一次的那个数。
要求以 O(logN) 时间复杂度进行求解,因此不能遍历数组并进行异或操作来求解,这么做的时间复杂度为 O(N)。
令 index 为 Single Element 在数组中的位置。在 index 之后,数组中原来存在的成对状态被改变。如果 m 为偶数,并且 m + 1 < index,那么 nums[m] == nums[m + 1];m + 1 >= index,那么 nums[m] != nums[m + 1]。
从上面的规律可以知道,如果 nums[m] == nums[m + 1],那么 index 所在的数组位置为 [m + 2, h],此时令 l = m + 2;如果 nums[m] != nums[m + 1],那么 index 所在的数组位置为 [l, m],此时令 h = m。
因为 h 的赋值表达式为 h = m,那么循环条件也就只能使用 l < h 这种形式。
参考:Github —— 有序数组的Single Element
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
int singleNonDuplicate(vector<int>& nums) {
int n = nums.size();
int l = 0, h = n - 1;
while (l < h) {
int mid = l + (h - l) / 2;
if (mid % 2 == 1) { /// 保证查找的区间是奇数个元素, 即 l、mid、h都在偶数位
mid --;
}
if (nums[mid] == nums[mid+1]) {
l = mid + 2;
} else {
h = mid;
}
}
return nums[l];
}
};
|
\278. First Bad Version
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public:
int firstBadVersion(int n) {
int l = 1, h = n;
while (l < h) {
int mid = l + (h - l) / 2;
if (isBadVersion(mid)) {
h = mid;
} else {
l = mid + 1;
}
}
return l;
}
};
|
\153. Find Minimum in Rotated Sorted Array
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public:
int findMin(vector<int>& nums) {
int l = 0, h = nums.size() - 1;
while (l < h) {
int m = l + (h - l) / 2;
if (nums[m] <= nums[h]) h = m;
else l = m+1;
}
return nums[l];
}
};
|
\34. Find First and Last Position of Element in Sorted Array
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if (nums.empty()) return {-1, -1};
int first = binarySearch(nums, target); // 第一个 可能=target的值的索引
int last = binarySearch(nums, target+1) - 1; // 第二个可能=target的值的索引
if(first == nums.size() || nums[first] != target) {
// 找到的第一个元素nums[first]不是目标值 或者 已经是数组最后一个数了
return {-1, -1};
} else {
return {first, last};
}
}
int binarySearch(vector<int> &nums, int target) {
int l = 0, h = nums.size(); // 注意h的值
while (l < h) {
int m = l + (h - l) / 2;
if(nums[m] >= target) h = m;
else l = m + 1;
}
return l;
}
};
|
分治
搜索
动态规划
数学
数据结构相关
链表
树
栈和队列
哈希表
字符串
数组与矩阵
图
位运算
\461. Hamming Distance —— Easy
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public:
int hammingDistance(int x, int y) {
int z = x ^ y;
int res = 0;
while (z) {
if(z & 1) res ++;
z >>= 1;
}
return res;
}
};
|
\136. Single Number (Easy)
1
2
3
4
5
6
7
8
|
class Solution {
public:
int singleNumber(vector<int>& nums) {
int res = 0;
for (int x: nums) res ^= x;
return res;
}
};
|
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 **三次 。**请你找出并返回那个只出现了一次的元素。
分析:对于每个数的 每个二进制位求和,出现三次的数 其对应位二进制和一定是3的倍数(0也是),那么对该二进制位的和sum%3,若其结果为1,则 一定是出现一次的那个数对应的该二进制位为1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public:
int singleNumber(vector<int>& nums) {
int res = 0, sum;
for (int i=0; i<32; i++) {
sum = 0;
for (int x: nums) {
sum += ((x >> i) & 1); //(x>>i) & 1表示x的第i个二进制位
}
if(sum % 3) res = res | (1<<i);
}
return res;
}
};
|
\268. Missing Number (Easy)
1
2
3
4
5
6
7
8
9
10
11
|
class Solution {
public:
int missingNumber(vector<int>& nums) {
int res = 0;
/// n = nums.size(), 如果不缺少[0,n]的数 则res=0, 否则 res^i^nums[i]则是确实的nums[i]
for (int i=0; i<nums.size(); i++) {
res = res ^ i ^ nums[i];
}
return res ^ nums.size();
}
};
|
\260. Single Number III(Medium)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
/**
* 两个不相等的元素在位级表示上必定会有一位存在不同。
将数组的所有元素异或得到的结果为不存在重复的两个元素异或的结果。
diff &= -diff 得到出 diff 最右侧不为 0 的位,也就是不存在重复的两个元素在位级表示上最右侧不同的那一位,利用这一位就可以将两个元素区分开来。
*/
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
long diff = 0;
for (auto x: nums) diff ^= x;
diff &= -diff; // 得到最低位的1
vector<int>res(2);
for(int x: nums) {
if((x & diff) == 0) res[0] ^= x;
else res[1] ^= x;
}
return res;
}
};
|
\190. Reverse Bits (Easy)
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public:
uint32_t reverseBits(uint32_t n) {
uint32_t res = 0;
for (int i=0; i<32; i++) {
res = res << 1;
res = res | (n & 1);
n = n >> 1;
}
return res;
}
};
|
\231. Power of Two (Easy)
1
2
3
4
5
6
7
|
class Solution {
public:
bool isPowerOfTwo(int n) {
/// n中只有一个1存在则 是2的n次方。 100 & 011 = 0;
return n > 0 && (n & (n-1)) == 0;
}
};
|
\342. Power of Four (Easy)
1
2
3
4
5
6
7
|
class Solution {
public:
bool isPowerOfFour(int n) {
//这种数在二进制表示中有且只有一个奇数位为 1,例如 16(10000)。
return n > 0 && (n&(n-1)) == 0 && (n & 0b01010101010101010101010101010101) != 0;
}
};
|
#Tree_LeetCode
Tree
二叉树的遍历
94. Binary Tree Inorder Traversal
Morris遍历:https://zhuanlan.zhihu.com/p/101321696
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
|
/**
/** Definition for a binary tree node.
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
*/
/**
* 94. Binary Tree Inorder Traversal
* 分析: 栈 或 Morris遍历;时间复杂度O(n), 空间复杂度分别为O(n), O(1)
* 栈: 根节点左边的先全部加入栈 找到最左下的一个空节点, 然后打印栈顶节点,加入右子节点;继续迭代直到结束
* Morris 遍历 建立中序线索树
*/
// 00 递归
class Solution {
public:
vector<int> result;
void dfsInorderTravel(TreeNode* root) {
if(root == nullptr) return;
dfsInorderTravel(root->left);
result.push_back(root->val);
dfsInorderTravel(root->right);
}
vector<int> inorderTraversal(TreeNode* root) {
dfsInorderTravel(root);
return result;
}
};
// 01 栈
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result; // 存储结果序列
stack<const TreeNode*> s;
const TreeNode *p = root;
while(!s.empty() || p != nullptr) {
/// 栈非空 或 根节点非空
if(p != nullptr) {
s.push(p);
p = p->left;
} else {
p = s.top();
s.pop();
result.push_back(p->val);
p = p->right;
}
}
return result;
}
};
/// 02 Morros遍历
//morris遍历的实质: 建立一种机制,对于没有左子树的节点只到达一次,对于有左子树的节点会到达两次
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
TreeNode *cur = root, *prev = nullptr;
while (cur != nullptr) {
/// 中序, 左根右 (建立中序线索树)
/// 先检查是否存在左子树
if (cur->left == nullptr) { // 不存在左子树
result.push_back(cur->val);//保存要打印的父节点的值
prev = cur; // 临时存储父节点,便于后面打印右子节点
cur = cur->right;
} else { // 遍历左子树,查找root的前驱
TreeNode *node = cur->left;
while (node->right != nullptr && node->right != cur) { ///root的前驱为left tree的最右边的元素
node = node->right;
}
if (node->right == nullptr) { // 还没线索化,则建立线索
node->right = cur;
cur = cur->left;
} else { // 已经线索化,则访问节点,并删除线索
result.push_back(cur->val);
node->right = nullptr;
prev = cur;
cur = cur->right;
}
}
}
return result;
}
};
|
144. Binary Tree Preorder Traversal
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
|
// 00 递归
class Solution {
public:
vector<int> result;
void dfsPreorderTravel(TreeNode* root) {
if(root == nullptr) return;
result.push_back(root->val);
dfsPreorderTravel(root->left);
dfsPreorderTravel(root->right);
}
vector<int> preorderTraversal(TreeNode* root) {
dfsPreorderTravel(root);
return result;
}
};
// 01 栈
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result; // 存储结果序列
stack<const TreeNode*> s;
if(root != nullptr) s.push(root);
while(!s.empty()) {
const TreeNode *p = s.top();
s.pop();
result.push_back(p->val);
if(p->right != nullptr) s.push(p->right);
if(p->left != nullptr) s.push(p->left);
}
return result;
}
};
// 02 Morris遍历
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
TreeNode *cur = root, *prev = nullptr;
while (cur != nullptr) {
/// 前序遍历: 根左右(建立前序线索树)
//先检查是否存在左子树
if(cur->left == nullptr) {
// 不存在左子树
result.push_back(cur->val);
prev = cur; // cur刚刚被访问过
cur = cur->right;
} else {
// 存在左子树
TreeNode *node = cur->left; // node为左子树的根节点
while(node->right != nullptr && node->right != cur) {
node = node->right;
}
if(node->right == nullptr) { // 还没线索化,则建立线索
result.push_back(cur->val); //仅这里与中序不同
prev = cur; // cur刚刚被访问过
node->right = cur;
cur = cur->left;
} else { // 已经线索化,则删除线索
node->right = nullptr;
cur = cur->right;
}
}
}
return result;
}
};
|
145. Binary Tree Postorder Traversal
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
//栈
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int> result;
stack<const TreeNode*>s;
// p: 正在访问的节点,刚刚访问过的节点
const TreeNode *p = root, *q = nullptr;
do {
while(p != nullptr) {
s.push(p);
p = p->left;
}
q = nullptr;
while(!s.empty()) {
p = s.top();
s.pop();
if(p->right == q) {// 右孩子不存在或已被访问,则访问它
result.push_back(p->val);
q = p;
} else {
// 存在右孩子,则不能访问当前节点
s.push(p);
p = p->right; // 先处理右子树
break;
}
}
} while (!s.empty());
return result;
}
};
// TODO:Morris遍历 (较前序 中序 复杂)
|
102. Binary Tree Level Order Traversal
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
|
// 递归版
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> result;
travel(root, 1, result);
return result;
}
void travel(TreeNode* root, int level, vector<vector<int>> &result) {
if(root == nullptr) return;
if(level > result.size()) {
result.push_back(vector<int>());
}
result[level-1].push_back(root->val);
travel(root->left, level+1, result);
travel(root->right, level+1, result);
}
};
// 迭代版
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> result;
queue<TreeNode*> current, next;
if(root == nullptr) {
return result;
} else {
current.push(root);
}
while(!current.empty()) {
vector<int> level; // 存储一层里的元素
while(!current.empty()) {
TreeNode *node = current.front();
current.pop();
level.push_back(node->val);
if(node->left != nullptr) next.push(node->left);
if(node->right != nullptr) next.push(node->right);
}
result.push_back(level);
swap(next, current); // current = next, next 为空队列
}
return result;
}
};
|
107. Binary Tree Level Order Traversal II
Example 1:

1
2
|
Input: root = [3,9,20,null,null,15,7]
Output: [[15,7],[9,20],[3]]
|
分析: 上一题 最后reverse一下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> result;
queue<TreeNode*> current, next;
if(root == nullptr) {
return result;
} else {
current.push(root);
}
while(!current.empty()) {
vector<int> level; // 存储一层里的元素
while(!current.empty()) {
TreeNode *node = current.front();
current.pop();
level.push_back(node->val);
if(node->left != nullptr) next.push(node->left);
if(node->right != nullptr) next.push(node->right);
}
result.push_back(level);
swap(next, current); // current = next, next 为空队列
}
reverse(result.begin(), result.end());
return result;
}
};
|
\103. Binary Tree Zigzag Level Order Traversal
Given the root of a binary tree, return the zigzag level order traversal of its nodes' values. (i.e., from left to right, then right to left for the next level and alternate between).
Example 1:

1
2
|
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[20,9],[15,7]]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
|
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> result;
queue<TreeNode*> current, next;
bool left_to_right = true;
if(root == nullptr) {
return result;
} else {
current.push(root);
}
while(!current.empty()) {
vector<int> level; // 存储一层里的元素
while(!current.empty()) {
TreeNode *node = current.front();
current.pop();
level.push_back(node->val);
if(node->left != nullptr) next.push(node->left);
if(node->right != nullptr) next.push(node->right);
}
if(left_to_right == false) {
reverse(level.begin(), level.end());
}
result.push_back(level);
left_to_right = !left_to_right;
swap(next, current); // current = next, next 为空队列
}
return result;
}
};
// 内存优化
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> result;
queue<TreeNode*> current;
bool left_to_right = true;
if(root == nullptr) {
return result;
} else {
current.push(root);
}
while(!current.empty()) {
vector<int> level; // 存储一层里的元素
int num = current.size();
while(num--) { // num表示每一层的节点个数
TreeNode *node = current.front();
current.pop();
level.push_back(node->val);
if(node->left != nullptr) current.push(node->left);
if(node->right != nullptr) current.push(node->right);
}
if(left_to_right == false) {
reverse(level.begin(), level.end());
}
result.push_back(level);
left_to_right = !left_to_right;
}
return result;
}
};
|
\99. Recover Binary Search Tree
You are given the root of a binary search tree (BST), where the values of exactly two nodes of the tree were swapped by mistake. Recover the tree without changing its structure.
Example 1:

1
2
3
|
Input: root = [1,3,null,null,2]
Output: [3,1,null,null,2]
Explanation: 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.
|
Example 2:

1
2
3
|
Input: root = [3,1,4,null,null,2]
Output: [2,1,4,null,null,3]
Explanation: 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid.
|
Constraints:
- The number of nodes in the tree is in the range
[2, 1000].
-231 <= Node.val <= 231 - 1
Follow up: A solution using O(n) space is pretty straight-forward. Could you devise a constant O(1) space solution?
分析:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
// 时间复杂度O(n), 空间复杂度O(1)
class Solution {
public:
void recoverTree(TreeNode* root) {
pair<TreeNode*, TreeNode*> swap_pair;
TreeNode *prev = nullptr, *cur = root;
while(cur != nullptr) {
if(cur->left == nullptr) {
detect(swap_pair, prev, cur);
prev = cur;
cur = cur->right;
} else {
// 存在左子树
TreeNode* node = cur->left;
while(node->right != nullptr && node->right != cur) { // 查找前驱
node = node->right;
}
if(node->right == nullptr) {
// 没有线索化,建立线索
node->right = cur;
cur = cur->left;
} else {
// 已经建立了线索,则删除线索
node->right = nullptr;
detect(swap_pair, prev, cur);
prev = cur; // 访问过
cur = cur->right;
}
}
}
swap(swap_pair.first->val, swap_pair.second->val);
}
void detect(pair<TreeNode*, TreeNode*> &swap_pair, TreeNode* prev, TreeNode* cur) {
if(prev != nullptr && prev->val > cur->val) {
if (swap_pair.first == nullptr)
swap_pair.first = prev;
swap_pair.second = cur;
}
}
};
|
\100. Same Tree
Given the roots of two binary trees p and q, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
// 递归版
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if(!p && !q) return true;
if(!p || !q) return false; //剪枝
return p->val == q->val && isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}
};
// 迭代版
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
stack<TreeNode *>s;
s.push(p);
s.push(q);
while(!s.empty()) {
p = s.top(); s.pop();
q = s.top(); s.pop();
if(!p && !q) continue; // 都为空
if(!p || !q) return false; // 有一个为空
if(p->val != q->val) return false;
s.push(p->left);
s.push(q->left);
s.push(p->right);
s.push(q->right);
}
return true;
}
};
|
\101. Symmetric Tree
Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).
Example 1:

1
2
|
Input: root = [1,2,2,3,4,4,3]
Output: true
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public:
bool isSymmetric(TreeNode* root) {
stack<TreeNode *>s;
TreeNode *p = root->left, *q = root->right;
s.push(p), s.push(q);
while(!s.empty()) {
p = s.top(); s.pop();
q = s.top(); s.pop();
if(!p && !q) continue; // 都为空
if(!p || !q) return false; // 有一个为空
if(p->val != q->val) return false;
s.push(p->left);
s.push(q->right);
s.push(p->right);
s.push(q->left);
}
return true;
}
};
|
\110. Balanced Binary Tree
Given a binary tree, determine if it is height-balanced.
For this problem, a height-balanced binary tree is defined as:
a binary tree in which the left and right subtrees of every node differ in height by no more than 1.
Example 1:

1
2
|
Input: root = [3,9,20,null,null,15,7]
Output: true
|
Example 2:

1
2
|
Input: root = [1,2,2,3,3,null,null,4,4]
Output: false
|
Constraints:
- The number of nodes in the tree is in the range
[0, 5000].
-104 <= Node.val <= 104
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
// 时间复杂度 O(logn)
class Solution {
public:
bool isBalanced(TreeNode* root) {
return balanceHeight(root) >= 0;
}
int balanceHeight(TreeNode* root) {
if(root == nullptr) return 0;
int left = balanceHeight(root->left);
int right = balanceHeight(root->right);
if(left < 0 || right < 0 || abs(left-right) > 1) return -1;
return max(left, right)+1;
}
};
|
114. Flatten Binary Tree to Linked List
Example 1:

1
2
|
Input: root = [1,2,5,3,4,null,6]
Output: [1,null,2,null,3,null,4,null,5,null,6]
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
//时间复杂度O(n), 空间复杂度O(logn)
// 递归版
class Solution {
public:
void flatten(TreeNode* root) {
if(!root) return ;
flatten(root->left);
flatten(root->right);
if(root->left == nullptr) return;
TreeNode *node = root->left;
while(node->right != nullptr) // 找到根节点的前驱节点
node = node->right;
node->right = root->right;
root->right = root->left;
root->left = nullptr;
}
};
// 迭代版
class Solution {
public:
void flatten(TreeNode* root) {
if(root == nullptr) return;
stack<TreeNode *> s;
s.push(root);
while (!s.empty()) {
auto p = s.top(); s.pop();
if(p->right != nullptr) s.push(p->right);
if(p->left != nullptr) s.push(p->left);
p->left = nullptr;
if(!s.empty()) p->right = s.top();
}
}
};
|
\117. Populating Next Right Pointers in Each Node II
Given a binary tree
1
2
3
4
5
6
|
struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
|
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Example 1:

1
2
3
|
Input: root = [1,2,3,4,5,null,7]
Output: [1,#,2,3,#,4,5,7,#]
Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.
|
Constraints:
- The number of nodes in the tree is in the range
[0, 6000].
-100 <= Node.val <= 100
Follow-up:
- You may only use constant extra space.
- The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem.
分析:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
// 递归版; 时间复杂度O(n), 空间复杂度O(1)
/*
一旦在某层的节点之间建立了 \text{next}next 指针,那这层节点实际上形成了一个链表。因此,如果先去建立某一层的 \text{next}next 指针,再去遍历这一层,就无需再使用队列了。
基于该想法,提出降低空间复杂度的思路:如果第 ii 层节点之间已经建立 \text{next}next 指针,就可以通过 \text{next}next 指针访问该层的所有节点,同时对于每个第 ii 层的节点,我们又可以通过它的 \rm leftleft 和 \rm rightright 指针知道其第 i+1i+1 层的孩子节点是什么,所以遍历过程中就能够按顺序为第 i + 1i+1 层节点建立 \text{next}next 指针。
链接:https://leetcode-cn.com/problems/populating-next-right-pointers-in-each-node-ii/solution/tian-chong-mei-ge-jie-dian-de-xia-yi-ge-you-ce-15/
*/
class Solution {
public:
Node* connect(Node* root) {
connected(root);
return root;
}
void connected(Node* root) {
if(root == nullptr) return ;
Node dummy(-1);
for (Node *cur = root, *prev = &dummy; cur != nullptr; cur = cur->next) {
if(cur->left != nullptr) {
prev->next = cur->left;
prev = prev->next;
}
if(cur->right != nullptr) {
prev->next = cur->right;
prev = prev->next;
}
}
connected(dummy.next);
}
};
// 迭代版
class Solution {
public:
Node* connect(Node* root) {
Node* result = root;
while(root) {
Node* next = nullptr; // 下一层的第一个节点
Node* prev = nullptr; // 同一层的前一个节点
for( ; root != nullptr; root = root->next) {
if(next == nullptr) {
// 获得下一层的第一个节点
next = root->left ? root->left : root->right;
}
if(root->left != nullptr) {
if(prev != nullptr) // 避免Runtime error
prev->next = root->left;
prev = root->left;
}
if(root->right != nullptr) {
if(prev != nullptr) // 避免Runtime error
prev->next = root->right;
prev = root->right;
}
}
root = next;
}
return result;
}
};
|
\116. Populating Next Right Pointers in Each Node
上述代码同样适用于本题
二叉树的构建
\105. Construct Binary Tree from Preorder and Inorder Traversal
分析:前序和中序遍历 构建二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
return buildTreeByPreAndInorder(begin(preorder), end(preorder), begin(inorder), end(inorder));
}
template<typename InputIterator>
TreeNode* buildTreeByPreAndInorder(InputIterator pre_first, InputIterator pre_last, InputIterator in_first, InputIterator in_last) {
if (pre_first == pre_last) return nullptr;
if (in_first == in_last) return nullptr;
auto root = new TreeNode(*pre_first);
auto in_root_pos = find(in_first, in_last, *pre_first); // 查找前序遍历元素在中序遍历中的位置对应的iterator
auto left_size = distance(in_first, in_root_pos); // 左子树中的元素长度
auto next_pre_last = next(pre_first, left_size+1); // 下一个pre_last对应位置的iterator
root->left = buildTreeByPreAndInorder(next(pre_first), next_pre_last, in_first, in_root_pos);
root->right = buildTreeByPreAndInorder(next_pre_last, pre_last, next(in_root_pos), in_last);
return root;
}
};
|
\106. Construct Binary Tree from Inorder and Postorder Traversal
分析:后序和中序遍历 构建二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
return buildTreeByInorderAndPost(begin(inorder), end(inorder), begin(postorder), end(postorder));
}
template<typename InputIterator>
TreeNode* buildTreeByInorderAndPost(InputIterator in_first, InputIterator in_last, InputIterator post_first, InputIterator post_last) {
if (in_first == in_last) return nullptr;
if (post_first == post_last) return nullptr;
const auto val = *prev(post_last);
auto root = new TreeNode(val); // 以二叉树的根构建树
auto in_root_pos = find(in_first, in_last, val); // 查找后序遍历元素在中序遍历中的位置对应的iterator
auto left_size = distance(in_first, in_root_pos); // 左子树中的元素列表长度
auto post_left_last = next(post_first, left_size);
root->left = buildTreeByInorderAndPost(in_first, in_root_pos, post_first, post_left_last);
root->right = buildTreeByInorderAndPost(next(in_root_pos), in_last, post_left_last, prev(post_last));
return root;
}
};
|
二叉查找树
\96. Unique Binary Search Trees
Given an integer n, return *the number of structurally unique **BST'*s (binary search trees) which has exactly n nodes of unique values from 1 to n.
Example 1:

1
2
|
Input: n = 3
Output: 5
|
Example 2:
1
2
|
Input: n = 1
Output: 1
|
Constraints:
分析:见leetcode-cpp。 卡特兰数
$f(0) = 1, f(1) = 1$
$f(i) = \sum_{k=1}^i{f(k-1)}*{f(i-k)}, i\in[1,n]$
通项公式:$f(n) = \frac{C_{2n}^{n}}{n+1}$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
// f(i) = \sum f(k-1) * (f(i-k), k \in [1, i], i \in [1,n]
class Solution {
public:
int numTrees(int n) {
vector<int> f(n+1, 0);
f[0] = 1, f[1] = 1;
for(int i=2; i<=n; ++i) {
for(int k=1; k<=i; ++k) {
f[i] += f[k-1] * f[i-k];
}
}
return f[n];
}
};
class Solution {
public:
int numTrees(int n) {
long res = 1;
for(int i=n+1; i<=2*n; ++i) {
res = res * i / (i-n);
}
return res / (n+1);
}
};
|
\95. Unique Binary Search Trees II
Given an integer n, return *all the structurally unique **BST'*s (binary search trees), which has exactly n nodes of unique values from 1 to n. Return the answer in any order.
Example 1:

1
2
|
Input: n = 3
Output: [[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]
|
Example 2:
1
2
|
Input: n = 1
Output: [[1]]
|
Constraints:
分析:如上题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution {
public:
vector<TreeNode*> generateTrees(int n) {
return generate(1, n);
}
private:
vector<TreeNode*> generate(int start, int end) {
vector<TreeNode*> sub_tree;
if (start > end) {
sub_tree.push_back(nullptr);
return sub_tree;
}
for (int k = start; k <= end; ++k) {
vector<TreeNode*> left_sub_tree = generate(start, k-1);
vector<TreeNode*> right_sub_tree = generate(k+1, end);
for(auto i: left_sub_tree) {
for(auto j: right_sub_tree) {
TreeNode* node = new TreeNode(k);
node->left = i;
node->right = j;
sub_tree.push_back(node);
}
}
}
return sub_tree;
}
};
|
\98. Validate Binary Search Tree
Given the root of a binary tree, determine if it is a valid binary search tree (BST).
A valid BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- Both the left and right subtrees must also be binary search trees.
Example 1:

1
2
|
Input: root = [2,1,3]
Output: true
|
Example 2:

1
2
3
|
Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: The root node's value is 5 but its right child's value is 4.
|
Constraints:
- The number of nodes in the tree is in the range
[1, 104].
-231 <= Node.val <= 231 - 1
分析: 递归,注意node.val的范围。 lower upper的类型声明为 long
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public:
bool isValidBST(TreeNode* root) {
return isValidBST(root, LONG_MIN, LONG_MAX);
}
bool isValidBST(TreeNode* root, long lower, long upper) {
if(root == nullptr) return true;
return root->val > lower && root->val < upper
&& isValidBST(root->left, lower, root->val)
&& isValidBST(root->right, root->val, upper);
}
};
|
\108. Convert Sorted Array to Binary Search Tree
Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.
A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.
Example 1:

1
2
3
|
Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: [0,-10,5,null,-3,null,9] is also accepted:
|
Example 2:

1
2
3
|
Input: nums = [1,3]
Output: [3,1]
Explanation: [1,3] and [3,1] are both a height-balanced BSTs.
|
Constraints:
1 <= nums.length <= 104-104 <= nums[i] <= 104nums is sorted in a strictly increasing order.
分析:二分法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
return sortedArrayToBST(begin(nums), end(nums));
}
template<typename Iterator>
TreeNode* sortedArrayToBST(Iterator first, Iterator last) {
const auto length = distance(first, last);
if(length <= 0) return nullptr; // 当数组为空时,终止
auto mid = first + length/2;
TreeNode* root = new TreeNode(*mid);
root->left = sortedArrayToBST(first, mid);
root->right = sortedArrayToBST(mid+1, last);
return root;
}
};
|
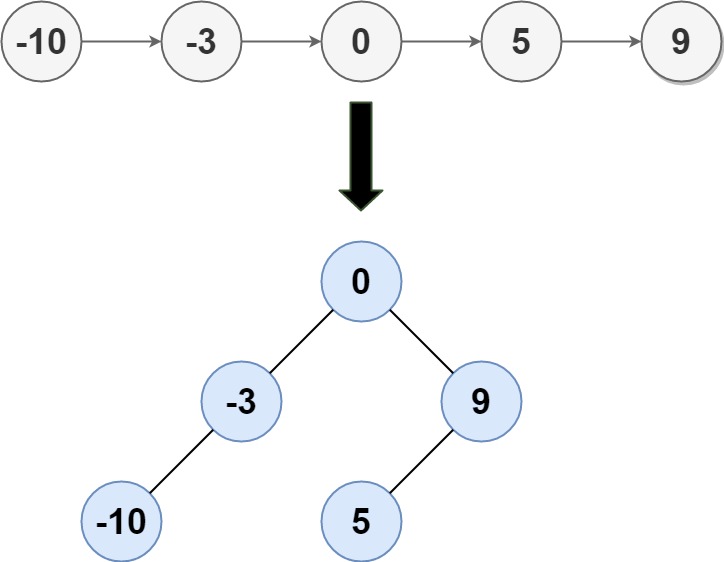
\109. Convert Sorted List to Binary Search Tree
Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height balanced BST.
For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.
Example 1:
1
2
3
|
Input: head = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: One possible answer is [0,-3,9,-10,null,5], which represents the shown height balanced BST.
|
Example 2:
1
2
|
Input: head = []
Output: []
|
Example 3:
1
2
|
Input: head = [0]
Output: [0]
|
Example 4:
1
2
|
Input: head = [1,3]
Output: [3,1]
|
Constraints:
- The number of nodes in
head is in the range [0, 2 * 104].
-105 <= Node.val <= 105
分析:类似于108. 自顶向下构建二叉搜索树。
方法2:自底向上 构建(二分法)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
// 时间复杂度O(n) 空间复杂度O(logn)
class Solution {
public:
TreeNode* sortedListToBST(ListNode* head) {
int length = 0;
ListNode* p = head;
while(p) {
++ length;
p = p->next;
}
return sortedListToBST(head, 0, length-1);
}
private:
TreeNode* sortedListToBST(ListNode*& list, int lower, int upper) {
if (lower > upper) return nullptr;
int mid = lower + (upper-lower) / 1;
TreeNode *left_tree = sortedListToBST(list, lower, mid-1);
TreeNode *root = new TreeNode(list->val);
root->left = left_tree;
list = list->next;
root->right = sortedListToBST(list, mid+1, upper);
return root;
}
};
|
二叉树的递归
搞懂 递归 与 深搜 的区别
\111. Minimum Depth of Binary Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
// 递归版
class Solution {
public:
int minDepth(TreeNode* root) {
return minDepth(root, false);
}
private:
static int minDepth(const TreeNode* root, bool hasbrother) {
if(root == nullptr) return hasbrother ? INT_MAX : 0;
return 1 + min(minDepth(root->left, root->right != nullptr),
minDepth(root->right, root->left != nullptr));
}
};
// 迭代版
class Solution {
public:
int minDepth(TreeNode* root) {
if(!root) return 0;
int result = INT_MAX;
stack<pair<TreeNode*, int>> node_depth;
node_depth.push(make_pair(root, 1));
while(!node_depth.empty()) {
TreeNode* node = node_depth.top().first;
int depth = node_depth.top().second;
node_depth.pop();
if(node->left == nullptr && node->right == nullptr) { // node为叶节点
result = min(result, depth);
}
if(node->left != nullptr && result > depth) { // result > depth 来作为剪枝条件
node_depth.push(make_pair(node->left, depth+1));
}
if(node->right != nullptr && result > depth) {
node_depth.push(make_pair(node->right, depth+1));
}
}
return result;
}
};
|
\112. Path Sum
Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.
A leaf is a node with no children.
Example 1:

1
2
|
Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
Output: true
|
分析:不需要打印路径,存在一条路径节点之和等于targetSum, 即打印true
1
2
3
4
5
6
7
8
9
10
|
class Solution {
public:
bool hasPathSum(TreeNode* root, int targetSum) {
if(!root) return false;
if(root->left == nullptr && root->right == nullptr)
return targetSum == root->val;
return hasPathSum(root->left, targetSum - root->val)
|| hasPathSum(root->right, targetSum - root->val);
}
};
|
\113. Path Sum II
Given the root of a binary tree and an integer targetSum, return all root-to-leaf paths where the sum of the node values in the path equals targetSum. Each path should be returned as a list of the node values, not node references.
A root-to-leaf path is a path starting from the root and ending at any leaf node. A leaf is a node with no children.
Example 1:

1
2
3
4
5
|
Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: [[5,4,11,2],[5,8,4,5]]
Explanation: There are two paths whose sum equals targetSum:
5 + 4 + 11 + 2 = 22
5 + 8 + 4 + 5 = 22
|
分析: 与上一题不同的是:需要打印出所有路径和等于targetSum的节点路径
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public:
vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
vector<int> cur; // 记录当前的路径
vector<vector<int> > result;
pathSum(root, targetSum, cur, result);
return result;
}
void pathSum(TreeNode* root, int dis, vector<int> &cur, vector<vector<int>> &result) {
if(!root) return ;
cur.push_back(root->val); // 添加到当前路径列表中
if(root->left == nullptr && root->right == nullptr) {
if(dis == root->val) {
result.push_back(cur);
}
}
pathSum(root->left, dis - root->val, cur, result);
pathSum(root->right, dis - root->val, cur, result);
cur.pop_back();
}
};
|
\124. Binary Tree Maximum Path Sum【Hard】
A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.
The path sum of a path is the sum of the node’s values in the path.
Given the root of a binary tree, return the maximum path sum of any non-empty path.
Example 1:

1
2
3
|
Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.
|
Example 2:

1
2
3
|
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.
|
Constraints:
- The number of nodes in the tree is in the range
[1, 3 * 104].
-1000 <= Node.val <= 1000
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public:
int maxPathSum(TreeNode* root) {
max_sum = INT_MIN;
dfs(root);
return max_sum;
}
private:
int max_sum; // max_sum 为路径和的最大值
int dfs(const TreeNode* root) {
if(!root) return 0;
int l = dfs(root->left);
int r = dfs(root->right);
int sum = root->val;
if(l > 0) sum += l;
if(r > 0) sum += r;
max_sum = max(max_sum, sum);
return max(l, r) > 0 ? // 左 右 子树的元素和较大值是否大于0,大于0则对整个和有利
max(l, r) + root->val : root->val;
}
};
|
\129. Sum Root to Leaf Numbers
You are given the root of a binary tree containing digits from 0 to 9 only.
Each root-to-leaf path in the tree represents a number.
- For example, the root-to-leaf path
1 -> 2 -> 3 represents the number 123.
Return the total sum of all root-to-leaf numbers. Test cases are generated so that the answer will fit in a 32-bit integer.
A leaf node is a node with no children.
Example 1:

1
2
3
4
5
6
|
Input: root = [1,2,3]
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.
|
Example 2:

1
2
3
4
5
6
7
|
Input: root = [4,9,0,5,1]
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.
|
Constraints:
- The number of nodes in the tree is in the range
[1, 1000].
0 <= Node.val <= 9- The depth of the tree will not exceed
10.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public:
int sumNumbers(TreeNode* root) {
return sumNumbers(root, 0);
}
private:
static int sumNumbers(TreeNode* root, int sum) {
if(!root) return 0;
if(root->left == nullptr && root->right == nullptr) {
return sum * 10 + root->val;
}
return sumNumbers(root->left, sum * 10 + root->val)
+ sumNumbers(root->right, sum * 10 + root->val);
}
};
|
Tree —— 其他题目
Easy
\235. Lowest Common Ancestor of a Binary Search Tree
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:

1
2
3
|
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.
|
Example 2:

1
2
3
|
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
// 利用BST的 性质, 左子树的节点值 < 根节点的值 < 右子树的节点值
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(!root) return nullptr;
if(root->val > max(p->val, q->val)) {
return lowestCommonAncestor(root->left, p, q);
} else if (root->val < min(p->val, q->val)) {
return lowestCommonAncestor(root->right, p, q);
} else { // 找到此区间
return root;
}
}
};
|
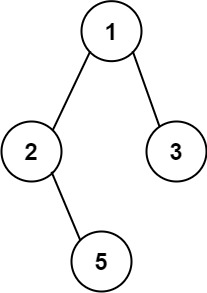
\257. Binary Tree Paths
Given the root of a binary tree, return all root-to-leaf paths in any order.
A leaf is a node with no children.
Example 1:
1
2
|
Input: root = [1,2,3,null,5]
Output: ["1->2->5","1->3"]
|
Example 2:
1
2
|
Input: root = [1]
Output: ["1"]
|
Constraints:
- The number of nodes in the tree is in the range
[1, 100].
-100 <= Node.val <= 100
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public:
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> result;
binaryTreePaths(root, "", result);
return result;
}
void binaryTreePaths(TreeNode* root, string s, vector<string> &result) {
if(!root) return ;
if(root->left == nullptr && root->right == nullptr) {
result.push_back(s + to_string(root->val));
}
if(root->left) {
binaryTreePaths(root->left, s + to_string(root->val) + "->", result);
}
if(root->right) {
binaryTreePaths(root->right, s + to_string(root->val) + "->", result);
}
}
};
|
\404. Sum of Left Leaves
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public:
int sumOfLeftLeaves(TreeNode* root) {
int sum = 0;
sumOfLeftLeaves(root, sum);
return sum;
}
void sumOfLeftLeaves(TreeNode* root, int &sum) {
if (!root) return ;
if(root->left && !root->left->left && !root->left->right) {
sum += root->left->val;
}
sumOfLeftLeaves(root->left, sum);
sumOfLeftLeaves(root->right, sum);
}
};
|
\501. Find Mode in Binary Search Tree
Given the root of a binary search tree (BST) with duplicates, return all the mode(s) (i.e., the most frequently occurred element) in it.
If the tree has more than one mode, return them in any order.
Assume a BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than or equal to the node’s key.
- The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
- Both the left and right subtrees must also be binary search trees.
Example 1:

1
2
|
Input: root = [1,null,2,2]
Output: [2]
|
Example 2:
1
2
|
Input: root = [0]
Output: [0]
|
Constraints:
- The number of nodes in the tree is in the range
[1, 104].
-105 <= Node.val <= 105
Follow up: Could you do that without using any extra space? (Assume that the implicit stack space incurred due to recursion does not count).
分析:利用二叉搜索树性质,本题中 左<=根<=右。 则利用prev记录上一个节点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution {
public:
vector<int> findMode(TreeNode* root) {
vector<int> result;
int num=1, max_num=0;
TreeNode* prev = nullptr;
findMode(root, prev, num, max_num, result);
return result;
}
private:
void findMode(TreeNode* node, TreeNode* &prev, int &num, int &max_num, vector<int> &res) {
if(!node) return;
findMode(node->left, prev, num, max_num, res);
// 中序遍历
if(prev != nullptr) { // prev非空 即不是第一个节点
num = (node->val == prev->val) ? num+1 : 1;
}
if(num >= max_num) {
if(num > max_num) res.clear();
res.push_back(node->val);
max_num = num;
}
prev = node; // 当前节点访问过了
findMode(node->right, prev, num, max_num, res);
}
};
|
\530. Minimum Absolute Difference in BST
Given the root of a Binary Search Tree (BST), return the minimum absolute difference between the values of any two different nodes in the tree.
Example 1:

1
2
|
Input: root = [4,2,6,1,3]
Output: 1
|
Example 2:

1
2
|
Input: root = [1,0,48,null,null,12,49]
Output: 1
|
Constraints:
- The number of nodes in the tree is in the range
[2, 104].
0 <= Node.val <= 105
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public:
int getMinimumDifference(TreeNode* root) {
TreeNode* prev = nullptr;
int res = INT_MAX;
getMinimumDifference(root, prev, res);
return res;
}
void getMinimumDifference(TreeNode* root, TreeNode* &prev, int &res) {
if(!root) return;
getMinimumDifference(root->left, prev, res);
if(prev != nullptr) {
res = min(res, root->val - prev->val);
}
prev = root;
getMinimumDifference(root->right, prev, res);
}
};
|
\543. Diameter of Binary Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public:
int diameterOfBinaryTree(TreeNode* root) {
int res = 0;
height(root, res);
return res - 1;
}
int height(TreeNode* root, int &res) {
if(!root) return 0;
int l = height(root->left, res);
int r = height(root->right, res);
if(1 + l + r > res) res = l + r + 1;
return 1 + max(l, r);
}
};
|
\563. Binary Tree Tilt
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public:
int findTilt(TreeNode* root) {
int res = 0;
tilt(root, res);
return res;
}
int tilt(TreeNode* root, int &sum) {
if(!root) return 0;
int l = tilt(root->left, sum);
int r = tilt(root->right, sum);
sum += abs(l - r);
return l + r + root->val;
}
};
|
\572. Subtree of Another Tree
Given the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.
A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node’s descendants. The tree tree could also be considered as a subtree of itself.
Example 1:
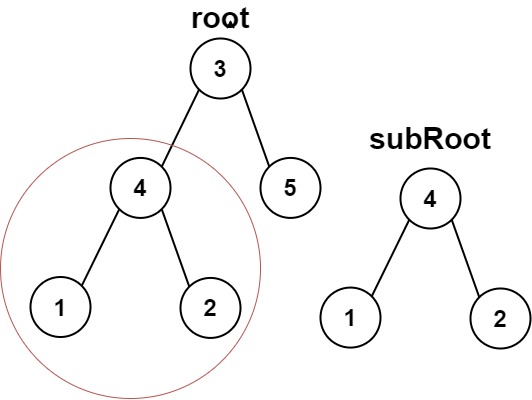
1
2
|
Input: root = [3,4,5,1,2], subRoot = [4,1,2]
Output: true
|
Example 2:
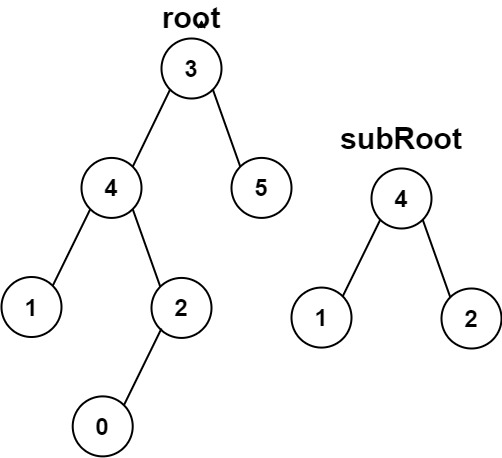
1
2
|
Input: root = [3,4,5,1,2,null,null,null,null,0], subRoot = [4,1,2]
Output: false
|
Constraints:
- The number of nodes in the
root tree is in the range [1, 2000].
- The number of nodes in the
subRoot tree is in the range [1, 1000].
-104 <= root.val <= 104-104 <= subRoot.val <= 104
分析:首先写出判断两棵树相等的函数isSame(), 计算subRoot的高度,然后在root中找出与 其高度相等的树 node,最后 用isSame() 比较node与subRoot
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
// 时间复杂度 O(m logn) m表示root的节点数量,n表示subRoot节点数量,空间复杂度 TODO
class Solution {
public:
bool isSubtree(TreeNode* root, TreeNode* subRoot) {
height(root, height(subRoot, -1));
for (auto node: nodes) {
if (isSame(node, subRoot))
return true;
}
return false;
}
private:
vector<TreeNode*> nodes;
int height(TreeNode* root, int h) {
if(!root) return 0;
int depth = max(height(root->left, h), height(root->right, h)) + 1;
if(depth == h) {
nodes.push_back(root);
}
return depth;
}
bool isSame(TreeNode* node1, TreeNode* node2) {
if (!node1 && !node2) return true;
if (!node1 || !node2) return false;
return node1->val == node2->val
&& isSame(node1->left, node2->left)
&& isSame(node1->right, node2->right);
}
};
|
\606. Construct String from Binary Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
class Solution {
public:
string tree2str(TreeNode* root) {
string res = to_string(root->val);
if(root->left) res += "(" + tree2str(root->left) + ")";
else if(root->right) res += "()";
if(root->right) res += "(" + tree2str(root->right) + ")";
return res;
}
};
// 栈
class Solution {
public:
string tree2str(TreeNode* root) {
string res = to_string(root->val);
stack<TreeNode*> stk({root});
while (!stk.empty()) {
TreeNode* node = stk.top();
stk.pop();
if(!node) {
res += ")";
continue;
}
if(node != root) {
res += "(" + to_string(node->val);
stk.push(nullptr);
}
if(!node->left && node->right) res += "()";
if(node->right) stk.push(node->right);
if(node->left) stk.push(node->left);
}
return res;
}
};
|
\617. Merge Two Binary Trees
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public:
TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
if(root1 && root2) {
TreeNode* root = new TreeNode(root1->val + root2->val);
root->left = mergeTrees(root1->left, root2->left);
root->right = mergeTrees(root1->right, root2->right);
return root;
} else {
return root1 ? root1 : root2;
}
}
};
|
\637. Average of Levels in Binary Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
queue<TreeNode*> q;
vector<double> res;
q.push(root);
while(!q.empty()) {
long sum = 0, sz= q.size();
for(int i=0; i<sz; ++i) {
TreeNode* node = q.front();
q.pop();
sum += node->val;
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
res.push_back(1.0 * sum / sz);
}
return res;
}
};
|
Given the root of a Binary Search Tree and a target number k, return true if there exist two elements in the BST such that their sum is equal to the given target.
Example 1:

1
2
|
Input: root = [5,3,6,2,4,null,7], k = 9
Output: true
|
Example 2:

1
2
|
Input: root = [5,3,6,2,4,null,7], k = 28
Output: false
|
Example 3:
1
2
|
Input: root = [2,1,3], k = 4
Output: true
|
Example 4:
1
2
|
Input: root = [2,1,3], k = 1
Output: false
|
Example 5:
1
2
|
Input: root = [2,1,3], k = 3
Output: true
|
Constraints:
- The number of nodes in the tree is in the range
[1, 104].
-104 <= Node.val <= 104root is guaranteed to be a valid binary search tree.-105 <= k <= 105
分析:题目要找BST中两个节点元素和 = k,仅利用BST节点元素值 可以直接转化为数组或不定序集合。先中序遍历加入到数组中,因为有序,所以O(n)实现两个元素和的值的计算 =k 则为true,如果直到两个指针相等,则返回false。 时间复杂度O(n),空间复杂度O(n)
BST, 利用性质 左 < 根 < 右。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
// [最好情况下]时间复杂度O(n logn) 空间复杂度O(n)
class Solution {
public:
bool findTarget(TreeNode* root, int k) {
return dfs(root, root, k);
}
private:
bool dfs(TreeNode* root, TreeNode* cur, int k) { // root代表原始BST,cur代表当前BST
if(!cur) return false;
return search(root, cur, k - cur->val) || dfs(root, cur->left, k) || dfs(root, cur->right, k);
}
bool search(TreeNode* root, TreeNode* cur, int k) {
if(!root) return false;
return (root != cur && root->val == k) || (k < root->val && search(root->left, cur, k)) ||
(k > root->val && search(root->right, cur, k));
}
};
|
\671. Second Minimum Node In a Binary Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public:
int findSecondMinimumValue(TreeNode* root) {
long sec_mini_val = LONG_MAX, minimum_val = root->val;
bool flag = false;
dfs(root, minimum_val, sec_mini_val, flag);
return flag ? sec_mini_val : -1;
}
private:
void dfs(TreeNode* root, const long min_val, long &sec_val, bool &flag) {
if(!root) return;
if(root->val > min_val && root->val < sec_val) {
flag = true;
sec_val = root->val;
return;
}
dfs(root->left, min_val, sec_val, flag);
dfs(root->right, min_val, sec_val, flag);
}
};
|
\559. Maximum Depth of N-ary Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
// BFS
class Solution {
public:
int maxDepth(Node* root) {
if(root == nullptr) return 0;
queue<Node*> q;
int depth = 0;
q.push(root);
while(!q.empty()) {
++depth;
int sz = q.size();
for(int i=0; i<sz; i++) {
auto node = q.front();
q.pop();
for(auto child: node->children) {
if(child != nullptr) q.push(child);
}
}
}
return depth;
}
};
//DFS
class Solution {
public:
int maxDepth(Node* root) {
if (!root) return 0;
int depth = 0;
for (auto child: root->children) {
depth = max(depth, maxDepth(child));
}
return 1 + depth;
}
};
|
\589. N-ary Tree Preorder Traversal
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
//DFS
class Solution {
public:
vector<int> preorder(Node* root) {
vector<int> result;
preorder(root, result);
return result;
}
private:
void preorder(Node* root, vector<int> &res) {
if(!root) return ;
res.push_back(root->val);
for(auto child: root->children) {
preorder(child, res);
}
}
};
// 栈
class Solution {
public:
vector<int> preorder(Node* root) {
vector<int> result;
if(!root) return result;
stack<Node*> stk;
stk.push(root);
while(!stk.empty()) {
Node* node = stk.top();
stk.pop();
result.push_back(node->val);
int sz = node->children.size();
for (int i=sz-1; i>=0; i--) {
if(node->children[i]) stk.push(node->children[i]);
}
}
return result;
}
};
|
\590. N-ary Tree Postorder Traversal
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
//DFS
class Solution {
public:
vector<int> postorder(Node* root) {
vector<int> result;
postorder(root, result);
return result;
}
private:
void postorder(Node* root, vector<int> &res) {
if(!root) return ;
for(auto child: root->children) {
postorder(child, res);
}
res.push_back(root->val);
}
};
//栈
class Solution {
public:
vector<int> postorder(Node* root) {
vector<int> result;
if(!root) return result;
stack<Node*> stk;
stk.push(root);
while(!stk.empty()) {
Node* node = stk.top();
stk.pop();
for(Node* child: node->children) {
if(child) stk.push(child);
}
result.push_back(node->val);
}
reverse(result.begin(), result.end());
return result;
}
};
|
\700. Search in a Binary Search Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
// DFS
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
TreeNode* res = nullptr;
bool exited = false;
searchBST(root, val, exited, res);
return res;
}
private:
void searchBST(TreeNode* root, int val, bool &exited, TreeNode* &res) {
if(!root || exited) return;
if(root->val > val) searchBST(root->left, val, exited, res);
else if (root->val < val) searchBST(root->right, val, exited, res);
else {
exited = true;
res = root;
}
}
};
// 迭代版
class Solution {
public:
TreeNode* searchBST(TreeNode* root, int val) {
while(root && root->val != val) {
root = (root->val > val) ? root->left : root->right;
}
return root;
}
};
|
\783. Minimum Distance Between BST Nodes
同530.
\703. Kth Largest Element in a Stream
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class KthLargest {
public:
priority_queue<int, vector<int>, greater<int> >pq;
int sz;
KthLargest(int k, vector<int>& nums) {
for(auto num: nums) {
pq.push(num);
if(pq.size() > k) pq.pop();
}
sz = k;
}
int add(int val) {
pq.push(val);
if(pq.size() > sz) pq.pop();
return pq.top();
}
};
|
\872. Leaf-Similar Trees
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
// dfs
class Solution {
public:
bool leafSimilar(TreeNode* root1, TreeNode* root2) {
vector<int> leaves1, leaves2;
dfs(root1, leaves1);
dfs(root2, leaves2);
return leaves1 == leaves2;
}
void dfs(TreeNode* root, vector<int> &res) {
if(!root) return;
if(!root->left && !root->right) res.push_back(root->val);
dfs(root->left, res);
dfs(root->right, res);
}
};
// 不保存叶子节点列表的方法:
/**
* 依次找出叶子节点, 一一比较,如果存在一个不同则 return false, 如果叶子节点都相同。
* 时间复杂度:O(log n)
*/
class Solution {
public:
bool leafSimilar(TreeNode* root1, TreeNode* root2) {
stack<TreeNode*> st1, st2;
st1.push(root1), st2.push(root2);
while (!st1.empty() && !st2.empty()) {
if(dfs(root1, st1) != dfs(root2, st2)) return false;
}
return st1.empty() && st2.empty(); // 这里不能直接返回true, 原因见下图
}
int dfs(TreeNode* root, stack<TreeNode*> &st) { // dfs() 找出叶子节点
while (true) {
TreeNode* node = st.top();
st.pop();
if(node->right) st.push(node->right);
if(node->left) st.push(node->left);
if(!node->left && !node->right) return node->val;
}
}
};
|
两棵树分别为: [3,5,1,6,7,4,2,null,null,null,null,null,null,9,11,null,null,8,10]
[3,5,1,6,2,9,8,null,null,7,4]
即 避免出现一棵树的叶子节点列表是另一棵树叶子节点列表的前缀列表 这种情况。
\897. Increasing Order Search Tree
Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
Example 1:
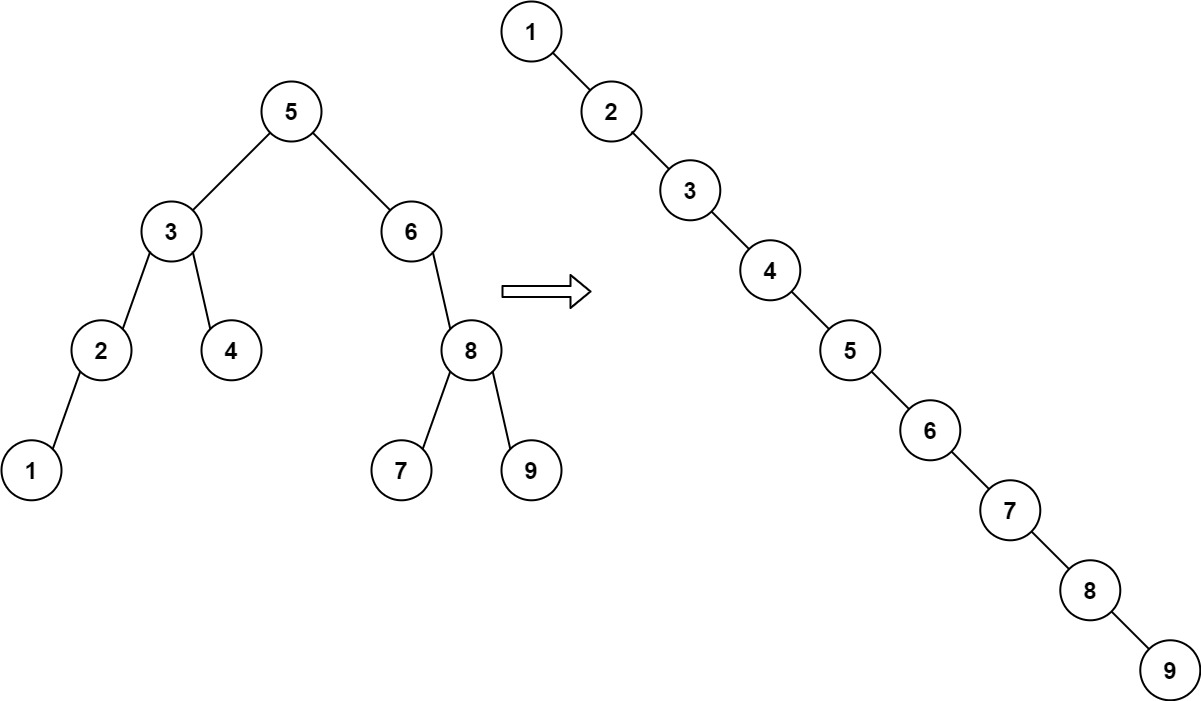
1
2
|
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
|
Example 2:
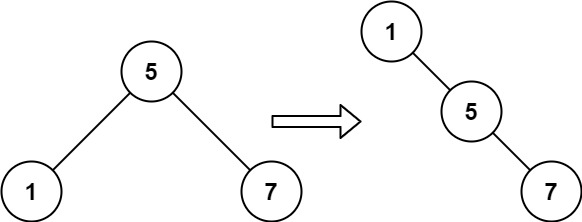
1
2
|
Input: root = [5,1,7]
Output: [1,null,5,null,7]
|
分析:
res = inorder(root->left) + root + inorder(root->right)
TreeNode* increasingBST(TreeNode* root, TreeNode* tail) tail是中序遍历中的下一个节点
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public:
TreeNode* increasingBST(TreeNode* root) {
return increasingBST(root, nullptr);
}
TreeNode* increasingBST(TreeNode* root, TreeNode* tail) {
if(!root) return tail;
TreeNode* res = increasingBST(root->left, root);
root->left = nullptr; // 最后构建的是右单链表,所以左子树 为空
root->right = increasingBST(root->right, tail);
return res;
}
};
|
\938. Range Sum of BST
分析:
方法1:中序遍历(只要是二叉树就可以用,不必要求是BST); 时间复杂度O(log n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
class Solution {
public:
long res = 0;
int rangeSumBST(TreeNode* root, int low, int high) {
if(!root) return 0;
if(root->val >= low && root->val <= high) res += root->val;
rangeSumBST(root->left, low, high);
rangeSumBST(root->right, low, high);
return res;
}
};
// 栈的写法
class Solution {
public:
int rangeSumBST(TreeNode* root, int low, int high) {
if(!root) return 0;
stack<TreeNode*>st;
st.push(root);
int res = 0;
while (!st.empty()) {
TreeNode* node = st.top();
st.pop();
if(node->val >= low && node->val <= high) res += node->val;
else { // 利用BST性质优化
if(node->val < low && node->right) st.push(node->right);
if(node->val > high && node->left) st.push(node->left);
continue;
}
if(node->right) st.push(node->right);
if(node->left) st.push(node->left);
}
return res;
}
};
// 方法2:用BST的性质 优化
class Solution {
public:
int rangeSumBST(TreeNode* root, int low, int high) {
if(!root) return 0;
int res = 0;
if(root->val >= low && root->val <= high) {
res += root->val + rangeSumBST(root->left, low, high) + rangeSumBST(root->right, low, high);
} else {
res += ((root->val < low) ? rangeSumBST(root->right, low, high) : 0)
+ ((root->val > high) ? rangeSumBST(root->left, low, high) : 0);
}
return res;
}
};
|
\965. Univalued Binary Tree
1
2
3
4
5
6
7
8
9
10
11
|
class Solution {
public:
bool isUnivalTree(TreeNode* root) {
int val = root->val;
return dfs(root, val);
}
bool dfs(TreeNode* root, const int val) {
if (!root) return true;
return val == root->val && dfs(root->left, val) && dfs(root->right, val);
}
};
|
\993. Cousins in Binary Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
// 使用pair<int, int> 存储x,y对应的树的父节点值与高度。 然后比较两者的关系
class Solution {
public:
bool isCousins(TreeNode* root, int x, int y) {
if(!root || root->val == x || root->val == y) return false;
pair<int, int> parent_depth1, parent_depth2;
func(root, x, y, 0, root->val, parent_depth1, parent_depth2);
return (parent_depth1.second == parent_depth2.second)
&& (parent_depth1.first != parent_depth2.first);
}
private:
void func(TreeNode* root, const int x, const int y, int depth, int parent, pair<int, int>&pd1, pair<int, int>&pd2) {
if(!root) return;
if(root->val == x) {
pd1.first = parent;
pd1.second = depth;
return;
}
if(root->val == y) {
pd2.first = parent;
pd2.second = depth;
return;
}
func(root->left, x, y, depth+1, root->val, pd1, pd2);
func(root->right, x, y, depth+1, root->val, pd1, pd2);
}
};
|
\1022. Sum of Root To Leaf Binary Numbers
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution {
public:
int sumRootToLeaf(TreeNode* root) {
vector<string> nums;
dfs(root, nums, "");
int sum = 0;
for(string s: nums) sum += binaryToTen(s);
return sum;
}
private:
void dfs(TreeNode* root, vector<string>& nums, string num) {
if(!root) return;
if(!root->left && !root->right) {
// 是叶节点
nums.push_back(num + to_string(root->val));
return;
}
dfs(root->left, nums, num + to_string(root->val));
dfs(root->right, nums, num + to_string(root->val));
}
int binaryToTen(string s) {
int num = 0;
for(int i=0; i<s.size(); i++) {
num = num * 2 + (s[i]-'0');
}
return num;
}
};
|
Medium
\199. Binary Tree Right Side View
Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.
Example 1:

1
2
|
Input: root = [1,2,3,null,5,null,4]
Output: [1,3,4]
|
分析: 层序遍历,保存每一层数组的最后一个元素
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
|
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<vector<int>> level_res;
vector<int>res;
levelTravel(root, 1, level_res);
for(int i=0; i<level_res.size(); i++) {
res.push_back(level_res[i][level_res[i].size()-1]);
}
return res;
}
private:
void levelTravel(TreeNode* root, int level, vector<vector<int>> &res) {
if(!root) return;
if(level > res.size()) {
res.push_back(vector<int>());
}
res[level-1].push_back(root->val);
levelTravel(root->left, level+1, res);
levelTravel(root->right, level+1, res);
}
};
// 改写前序遍历,时间复杂度O(n),空间复杂度O(logn)
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<int>res;
dfs(root, 1, res);
return res;
}
private:
void dfs(TreeNode* root, int level, vector<int> &res) {
if(!root) return;
if(level > res.size()) {
res.push_back(root->val);
}
dfs(root->right, level+1, res);
dfs(root->left, level+1, res);
}
};
// 栈
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<int>res;
if(!root) return res;
stack<pair<TreeNode*, int>> stk;
int depth = 1;
stk.push(make_pair(root, 1));
while(!stk.empty()) {
TreeNode* node=stk.top().first;
int height = stk.top().second;
stk.pop();
if(depth == height) {
res.push_back(node->val);
depth ++;
}
if(node->left) stk.push(make_pair(node->left, height+1));
if(node->right) stk.push(make_pair(node->right, height+1));
}
return res;
}
};
|
\222. Count Complete Tree Nodes
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
// 分析:当l_height == r_height时,说明是一颗满完全二叉树,否则分别计算左右子树的高度
// 时间复杂度:O(logn * logn) 空间复杂度O(logn)
class Solution {
public:
int countNodes(TreeNode* root) {
if(!root) return 0;
TreeNode* p_l=root, *p_r=root;
int l_height=1, r_height=1;
while (p_l = p_l->left) l_height ++;
while (p_r = p_r->right) r_height ++;
if(l_height == r_height) return pow(2, l_height) - 1; // 说明是一个满完全二叉树
return 1 + countNodes(root->left) + countNodes(root->right);
}
};
|
\230. Kth Smallest Element in a BST
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
// 时间复杂度 O(k) 取决于k的大小。 空间复杂度O(k)
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
val = k;
int res;
func(root, res);
return res;
}
void func(TreeNode* root, int &res) {
if(!root) return;
func(root->left, res);
-- val;
if(val == 0) {
res = root->val;
return;
}
func(root->right, res);
}
private:
int val;
};
// 栈
class Solution {
public:
int kthSmallest(TreeNode* root, int k) {
stack<TreeNode*>st;
while (root || !st.empty()) {
while (root) {
st.push(root);
root = root->left;
}
root = st.top();
if(--k == 0) {
return root->val;
}
st.pop();
root = root->right;
}
return root->val;
}
};
|
\236. Lowest Common Ancestor of a Binary Tree
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:

1
2
3
|
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.
|
Example 2:

1
2
3
|
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
|
Constraints:
- The number of nodes in the tree is in the range
[2, 105].
-109 <= Node.val <= 109- All
Node.val are unique.
p != qp and q will exist in the tree.
分析: TODO
1
2
3
4
5
6
7
8
9
10
11
|
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(!root || p == root || q == root) return root;
TreeNode* ltree = lowestCommonAncestor(root->left, p, q);
TreeNode* rtree = lowestCommonAncestor(root->right, p, q);
if(ltree && rtree) return root;
return ltree ? ltree : rtree;
}
};
|
\337. House Robber III
分析:直接比较 root->val 与间隔层的节点值之和 与 孩子节点这一层间隔的层级的元素值之和。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
// Time Limit Exceeded
class Solution {
public:
int rob(TreeNode* root) {
if(!root) return 0;
int sum = 0;
if(root->left) sum += rob(root->left->left) + rob(root->left->right);
if(root->right) sum += rob(root->right->left) + rob(root->right->right);
return max(sum + root->val, rob(root->left) + rob(root->right));
}
};
// 优化(使用引用)
class Solution {
public:
int rob(TreeNode* root) {
int l=0, r=0;
return rob(root, l, r);
}
private:
int rob(TreeNode* node, int& lsum, int &rsum) {
if(!node) return 0;
int ll=0, lr=0, rl=0, rr=0;
lsum = rob(node->left, ll, lr);
rsum = rob(node->right, rl, rr);
return max(node->val+ll+lr+rl+rr, lsum+rsum);
}
};
|
\429. N-ary Tree Level Order Traversal
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
// BFS
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
vector<vector<int>> res;
if(!root) return res;
queue<Node*> cur, next;
cur.push(root);
while (!cur.empty()) {
vector<int> level;
while(!cur.empty()) {
Node* node = cur.front();
cur.pop();
level.push_back(node->val);
for(Node *child: node->children) {
if(child) next.push(child);
}
}
res.push_back(level);
swap(next, cur);
}
return res;
}
};
// DFS
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
vector<vector<int>> res;
dfs(root, 1, res);
return res;
}
void dfs(Node* root, int level, vector<vector<int>>& res) {
if(!root) return;
if(level > res.size()) { // 当前层数组还没创建
res.push_back(vector<int>());
}
res[level-1].push_back(root->val);
for (auto child: root->children) {
dfs(child, level+1, res);
}
}
};
|
\437. Path Sum III
分析:这里与前面不同的是 可以不从根节点开始,只要求二叉树从上到下连续几个数的和 = target。
可以将每一个节点开始做连续求和看作一个子问题。
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public:
int pathSum(TreeNode* root, int targetSum) {
if(!root) return 0;
return sumFromRoot(root, 0, targetSum) + pathSum(root->left, targetSum) + pathSum(root->right, targetSum);
}
private:
int sumFromRoot(TreeNode* root, int pre, int targetSum) {
if(!root) return 0;
int curSum = pre + root->val;
return (curSum == targetSum) + sumFromRoot(root->left, curSum, targetSum) + sumFromRoot(root->right, curSum, targetSum);
}
};
|
\450. Delete Node in a BST
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key) {
if(!root) return nullptr;
if(root->val == key) { // 删除的是根节点
if(!root->left) return root->right;
if(!root->right) return root->left;
TreeNode *node = root->right;
while (node->left) node = node->left;
root->val = node->val;
root->right = deleteNode(root->right, root->val);
} else if(root->val < key) root->right = deleteNode(root->right, key);
else root->left = deleteNode(root->left, key);
return root;
}
};
|
\508. Most Frequent Subtree Sum
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public:
vector<int> findFrequentTreeSum(TreeNode* root) {
vector<int> res;
unordered_map<int, int> m;
int maxCount = 0;
dfs(root, maxCount, m);
for (auto &item: m) {
if(item.second == maxCount) res.push_back(item.first);
}
return res;
}
private:
int dfs(TreeNode *root, int& maxCount, unordered_map<int, int> &m) {
if(!root) return 0;
int sum = root->val + dfs(root->left, maxCount, m) + dfs(root->right, maxCount, m);
maxCount = max(maxCount, ++m[sum]);
return sum;
}
};
|
\513. Find Bottom Left Tree Value
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
vector<vector<int>> res;
dfs(root, 1, res);
return res[res.size()-1][0];
}
void dfs(TreeNode* root, int level, vector<vector<int>>&res) {
if(!root) return;
if(level > res.size()) res.push_back(vector<int>());
res[level-1].push_back(root->val);
dfs(root->left, level+1, res);
dfs(root->right, level+1, res);
}
};
// 维持最底部的左节点的值
class Solution {
public:
int findBottomLeftValue(TreeNode* root) {
int maxHeight = 0, leftVal = root->val;
findBottomLeftVal(root, maxHeight, leftVal, 0);
return leftVal;
}
void findBottomLeftVal(TreeNode* root, int &maxHeight, int &leftVal, int height) {
if(!root) return;
if(height > maxHeight) {
maxHeight = height;
leftVal = root->val;
}
findBottomLeftVal(root->left, maxHeight, leftVal, height+1);
findBottomLeftVal(root->right, maxHeight, leftVal, height+1);
}
};
|
\515. Find Largest Value in Each Tree Row
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
vector<int> res;
dfs(root, 1, res);
return res;
}
void dfs(TreeNode* root, int depth, vector<int>&res) {
if(!root) return;
if(depth > res.size()) {
res.push_back(INT_MIN);
}
if(root->val > res[depth-1]) res[depth-1] = root->val;
dfs(root->left, depth+1, res);
dfs(root->right, depth+1, res);
}
};
|
\538. Convert BST to Greater Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public:
TreeNode* convertBST(TreeNode* root) {
TreeNode* p = root;
int sum=0;
dfs(p, sum);
return root;
}
int dfs(TreeNode* node, int &sum) {
if(!node) return 0;
dfs(node->right, sum);
sum += node->val;
node->val = sum;
dfs(node->left, sum);
return sum;
}
};
|
\623. Add One Row to Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
TreeNode* addOneRow(TreeNode* root, int val, int depth) {
TreeNode* p = root;
if(depth == 1) {
TreeNode* node = new TreeNode(val);
node->left = p;
node->right = nullptr;
return node;
}
dfs(p, val, depth, 1);
return root;
}
void dfs(TreeNode* root, int val, int depth, int curDepth) {
if(!root) return;
if(curDepth == depth-1) {
TreeNode* node = new TreeNode(val);
TreeNode* node2 = new TreeNode(val);
node->left = root->left;
node2->right = root->right;
root->left = node;
root->right = node2;
}
dfs(root->left, val, depth, curDepth+1);
dfs(root->right, val, depth, curDepth+1);
}
};
|
\652. Find Duplicate Subtrees
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public:
vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {
vector<TreeNode*> res;
unordered_map<string, int> m;
dfs(root, m, res);
return res;
}
string dfs(TreeNode* root, unordered_map<string, int>& m, vector<TreeNode*> &res) {
if(!root ) return "";
string s = to_string(root->val) + "," + dfs(root->left, m, res) + "," + dfs(root->right, m, res);
if(++m[s] == 2) res.push_back(root);
return s;
}
};
|
\655. Print Binary Tree
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public:
vector<vector<string>> printTree(TreeNode* root) {
int height = getHeight(root);
int c = pow(2, height)-1;
vector<string> temp(c, "");
vector<vector<string>>res (height, temp);
replaceVal(root, 0, c-1, res, 0);
return res;
}
inline int getHeight(TreeNode* root) {
if(!root) return 0;
return 1 + max(getHeight(root->left), getHeight(root->right));
}
void replaceVal(TreeNode* root, int l, int r, vector<vector<string>> &res, int height) {
if(!root) return;
if(l > r) return;
int mid = (l + r) / 2;
res[height][mid] = to_string(root->val);
replaceVal(root->left, l, mid-1, res, height+1);
replaceVal(root->right, mid+1, r, res, height+1);
}
};
|
\662. Maximum Width of Binary Tree
Given the root of a binary tree, return the maximum width of the given tree.
The maximum width of a tree is the maximum width among all levels.
The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes are also counted into the length calculation.
It is guaranteed that the answer will in the range of 32-bit signed integer.
Example 1:
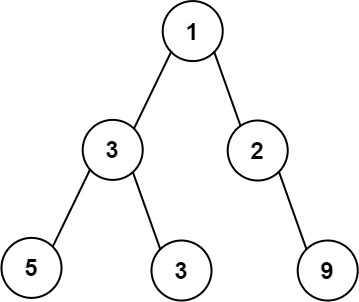
1
2
3
|
Input: root = [1,3,2,5,3,null,9]
Output: 4
Explanation: The maximum width existing in the third level with the length 4 (5,3,null,9).
|
Example 2:
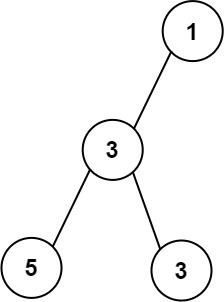
1
2
3
|
Input: root = [1,3,null,5,3]
Output: 2
Explanation: The maximum width existing in the third level with the length 2 (5,3).
|
Example 3:
1
2
3
|
Input: root = [1,3,2,5]
Output: 2
Explanation: The maximum width existing in the second level with the length 2 (3,2).
|
Example 4:
1
2
3
|
Input: root = [1,3,2,5,null,null,9,6,null,null,7]
Output: 8
Explanation: The maximum width existing in the fourth level with the length 8 (6,null,null,null,null,null,null,7).
|
Constraints:
- The number of nodes in the tree is in the range
[1, 3000].
-100 <= Node.val <= 100
分析:开始想到的是 层序遍历 并将一些只有左孩子或者右孩子的那一层加入nullptr,但是不能处理 example 4这样的情况。 下面巧妙的转化成 利用二叉树根与孩子的 2*n+1, 2n+2 索引性质。 还是层序遍历(BFS),不同的是,先获得每一层第一个节点的索引 作为left,然后遍历这一层,获得最后一个节点的索引作为right, 这就是当前层的宽度, 取所有层宽度中的最大值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
queue<pair<TreeNode*, unsigned long long>>que;
que.push({root, 0});
int max_width = 0;
while (!que.empty()) {
int sz = que.size();
unsigned long long right = 0, left = que.front().second;
while (sz--) {
pair<TreeNode *, unsigned long long> node = que.front();
que.pop();
right = node.second;
if (node.first->left) que.push({node.first->left, 2 * right + 1});
if (node.first->right) que.push({node.first->right, 2 * right + 2});
}
max_width = max(max_width, int(right-left+1));
}
return max_width;
}
};
|
Linked List
Easy
\21. Merge Two Sorted Lists
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
|
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
ListNode dummy(-1); // 头节点
ListNode *prev = &dummy, *p1=l1, *p2=l2;
while(p1 && p2) {
int val;
if(p1->val <= p2->val) {
val = p1->val;
p1 = p1->next;
} else {
val = p2->val;
p2 = p2->next;
}
prev->next = new ListNode(val); // 尾插法
prev = prev->next; // 后移
}
if(p1) prev->next = p1;
if(p2) prev->next = p2;
return dummy.next;
}
};
// 递归 混合插入节点
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
if(!l1) return l2;
if(!l2) return l1;
if(l1->val < l2->val) {
l1->next = mergeTwoLists(l1->next, l2);
return l1;
} else {
l2->next = mergeTwoLists(l1, l2->next);
return l2;
}
}
};
// 去掉if语句的写法。 时间 beats 95%, 空间 beats 99%【少了判断语句】
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
if(!l1) return l2;
if(!l2) return l1;
ListNode* head = l1->val < l2->val ? l1 : l2;
ListNode* nohead = l1->val < l2->val ? l2 : l1;
head->next = mergeTwoLists(head->next, nohead);
return head;
}
};
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
// 以 l1 链表为结果链表
if(!l1 || (l2 && l1->val > l2->val)) swap(l1, l2);
if(l1) l1->next = mergeTwoLists(l1->next, l2);
return l1;
}
};
|
\141. Linked List Cycle
1
2
3
4
5
6
7
8
9
10
11
12
13
|
// 快慢指针 空间复杂度O(1)
class Solution {
public:
bool hasCycle(ListNode *head) {
ListNode *fast=head, *slow=head;
while (fast && fast->next) {
fast = fast->next->next;
slow = slow->next;
if (slow == fast) return true;
}
return false;
}
};
|
\160. Intersection of Two Linked Lists
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
// 时间复杂度O(m+n), 空间复杂度O(1)
// 分析:找到交叉的节点, 两条链表交叉拼接,如果有交叉点,则可以找到并返回;否则没有
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
if(!headA || !headB) return nullptr;
ListNode *p1 = headA, *p2 = headB;
while (p1 && p2 && p1 != p2) {
p1 = p1->next;
p2 = p2->next;
if(!p1 && !p2) return nullptr;
if(!p1) p1 = headB;
if(!p2) p2 = headA;
}
return p1;
}
};
// 分析:先计算两个链表长度,将当前节点都指向剩余为访问节点长度相同的第一个节点
// 时间复杂度O(max(m, n)),空间复杂度O(1)
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
int lA = getLength(headA), lB = getLength(headB);
int sub;
ListNode *p1=headA, *p2=headB;
if(lA > lB) {
sub = lA - lB;
while (sub--) p1 = p1->next;
} else {
sub = lB - lA;
while (sub--) p2 = p2->next;
}
while (p1 && p2 && p1 != p2) {
p1 = p1->next;
p2 = p2->next;
}
return p1;
}
int getLength(ListNode *node) {
int length = 0;
while (node) {
length ++;
node = node->next;
}
return length;
}
};
|
\234. Palindrome Linked List
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
public:
bool isPalindrome(ListNode* head) {
if(!head || !head->next) return true;
ListNode *fast = head->next, *slow = head;
while (fast && fast->next) { // fast 走两步,slow走一步
fast = fast->next->next;
slow = slow->next;
}
fast = slow->next;
ListNode *back = reverseList(fast);
while (back) {
if (back->val != head->val) break;
back = back->next;
head = head->next;
}
return back == nullptr;
}
ListNode* reverseList(ListNode *a) {
ListNode *prev = nullptr, *cur = a, *next;
while (cur != nullptr) {
next = cur->next;
cur->next = prev;
prev = cur;
cur = next;
}
return prev;
}
};
|
\328. Odd Even Linked List
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
// 奇偶链表
class Solution {
public:
ListNode* oddEvenList(ListNode* head) {
if(!head && !head->next) return head;
ListNode *dummy = new ListNode(-1);
ListNode *odd = head, *even = head->next, *evenHead = even;
while (odd->next && even->next) {
odd->next = even->next;
odd = odd->next;
even->next = odd->next;
even = even->next;
}
odd->next = evenHead;
return head;
}
};
|
\705. Design HashSet
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
|
// 超大数组, time beats 84%, memory beats 44%
class MyHashSet {
public:
MyHashSet():res(1e6+1, false) {
}
void add(int key) {
res[key] = true;
}
void remove(int key) {
res[key] = false;
}
bool contains(int key) {
return res[key];
}
private:
vector<bool>res;
};
// 类似bitmap的结构
/* 使用 int 中的每一位代表一个位置。
由于数据范围为 0 <= key <= 10^6,我们最多需要的 int 数量不会超过 40000。
因此我们可以建立一个 buckets 数组,数组装载的 int 类型数值。
先对 key 进行 key / 32,确定当前 key 所在桶的位置(大概位置)
再对 key 进行 key % 32,确定当前 key 所在桶中的哪一位(精确位置)
根据位运算对「精确位置」进行修改。
*/
class MyHashSet {
public:
MyHashSet():res(4e4+1, 0) {
}
void setVal(int bucket, int loc, bool x) {
if(x) {
int u = res[bucket] | (1 << loc);
res[bucket] = u;
} else {
int u = res[bucket] & ~(1 << loc);
res[bucket] = u;
}
}
bool getVal(int bucket, int loc) {
int u = (res[bucket] >> loc) & 1;
return u == 1;
}
void add(int key) {
int bucketIdx = key / 32;
int bitIdx = key % 32;
setVal(bucketIdx, bitIdx, true);
}
void remove(int key) {
int bucketIdx = key / 32;
int bitIdx = key % 32;
setVal(bucketIdx, bitIdx, false);
}
bool contains(int key) {
int bucketIdx = key / 32;
int bitIdx = key % 32;
return getVal(bucketIdx, bitIdx);
}
private:
vector<int> res;//改成 int res[int(4e4+5)]={0}; 后,time beats 99%
};
|
\706. Design HashMap
\876. Middle of the Linked List
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
class Solution {
public:
ListNode* middleNode(ListNode* head) {
ListNode *cur = head;
int length = 0;
while (cur) {
++ length;
cur = cur->next;
}
length = length / 2;
while (length--) {
head = head->next;
}
return head;
}
};
// 双指针
class Solution {
public:
ListNode* middleNode(ListNode* head) {
if(!head || !head->next) return head;
ListNode *fast=head->next, *slow=head;
while (fast && fast->next) {
fast = fast->next->next;
slow = slow->next;
}
if(fast && !fast->next) slow = slow->next;
return slow;
}
};
|
\1290. Convert Binary Number in a Linked List to Integer
1
2
3
4
5
6
7
8
9
10
11
|
class Solution {
public:
int getDecimalValue(ListNode* head) {
int num = 0;
while (head) {
num = num * 2 + head->val;
head = head->next;
}
return num;
}
};
|
Medium
\2. Add Two Numbers
分析:模拟手算 + 尾插法(头节点)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode dummy(-1); //头节点
ListNode* pre = &dummy;
int carry = 0;
for(ListNode* p1=l1, *p2=l2; p1 || p2; p1= p1 ? p1->next : nullptr, p2=p2 ? p2->next : nullptr, pre=pre->next) {
const int ai = (p1 == nullptr) ? 0 : p1->val;
const int bi = (p2 == nullptr) ? 0 : p2->val;
const int val = (ai + bi + carry) % 10;
carry = (ai + bi + carry) / 10;
pre->next = new ListNode(val); // 尾插法
}
if(carry > 0) pre->next = new ListNode(carry);
return dummy.next;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
// 二级指针
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode **cur = &head; // 二级指针,指向第一个节点的地址
ListNode *entry = head;
for (int i=1; i<n; i++) {
entry = entry->next;
}
while (entry->next != nullptr) {
cur = &((*cur)->next);
entry = entry->next;
}
(*cur) = (*cur)->next;
return head;
}
};
// 快慢指针
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* fast=head, *slow=head;
while (n--) fast = fast->next;
if(!fast) { // 删除头节点的情况,即 n=length
return head->next;
}
while (fast->next) {
fast = fast->next;
slow = slow->next;
}
slow->next = slow->next->next;
return head;
}
};
|
\24. Swap Nodes in Pairs
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode* slow, *fast, **pp=&head;
while ((slow=*pp) && (fast=slow->next)) {
slow->next = fast->next;
fast->next = slow;
*pp = fast;
pp = &(slow->next);
}
return head;
}
};
|
\61. Rotate List
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
// 时间复杂度O(n)
class Solution {
public:
ListNode* rotateRight(ListNode* head, int k) {
if(!head) return nullptr;
ListNode *p = head, *prev, *res;
int length = 0;
while (p) {
++ length;
p = p->next;
}
int num = length-k%length;
if(num == length) return head;
p = head;
while (num--) {
prev = p;
p = p->next;
}
prev->next = nullptr;
prev = p;
while (p->next) {
p = p->next;
}
p->next = head;
return prev;
}
};
// 先改成环,然后重新连接
class Solution {
public:
ListNode* rotateRight(ListNode* head, int k) {
if(!head) return nullptr;
ListNode *tail = head;
int length = 1;
while (tail->next) {
++ length;
tail = tail->next;
}
tail->next = head; // 先改成单向环
int num = length-k%length;
for(int i=0; i<num; i++) {
tail = tail->next;
}
head = tail->next;
tail->next = nullptr;
return head;
}
};
|
\82. Remove Duplicates from Sorted List II
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
// 头节点,用三个指针prev, cur, next 时间复杂度O(n),空间复杂度O(1)
class Solution {
public:
ListNode* deleteDuplicates(ListNode* head) {
ListNode *dummy = new ListNode(-1);// 头节点
dummy->next = head;
ListNode *prev=dummy, *cur=head, *next;
while (cur) {
next = cur->next;
if(next && cur->val == next->val) {
while (next && cur->val == next->val) {
next = next->next;
cur = cur->next;
}
cur = next;
prev->next = next;
continue;
}
// 处理下一个重复元素
prev = cur;
cur = next;
}
return dummy->next;
}
};
|
\86. Partition List
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
// 分析:最直接的想法:将<x的节点放在一条链表中,另外的节点保留在原链表,然后拼接输出
class Solution {
public:
ListNode* partition(ListNode* head, int x) {
ListNode *dummy = new ListNode(-1);
ListNode *dummy0 = new ListNode(0);
dummy->next = head;
ListNode* p = head, *prev = dummy, *cur=dummy0;
while (p) {
if(p->val < x) {
cur->next = p;
cur = cur->next;
prev->next = p->next;
} else // 只有在不小于x时, prev才会变化
prev = p;
p = p->next;
}
cur->next = dummy->next;
return dummy0->next;
}
};
// 使用两个链表
class Solution {
public:
ListNode* partition(ListNode* head, int x) {
ListNode *ftdummy = new ListNode(0), *bddummy = new ListNode(0);
ListNode *fp = ftdummy, *bp = bddummy, *p = head;
while (p) {
if (p->val < x) fp->next = p, fp = fp->next;
else bp->next = p, bp = bp->next;
p = p->next;
}
fp->next = bddummy->next, bp->next = nullptr;
return ftdummy->next;
}
};
|
\92. Reverse Linked List II
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
class Solution {
public:
ListNode* reverseBetween(ListNode* head, int left, int right) {
ListNode *dummy = new ListNode(INT_MIN);
dummy->next = head;
ListNode *prev = dummy, *cur = head, *a;
while(right--) {
left--;
if(!left) a = cur;
if(left > 0) prev = cur;
cur = cur->next;
}
ListNode* pre = reverseList(nullptr, a, cur);
prev->next = pre;
while (pre->next) pre = pre->next;
pre->next = cur;
return dummy->next;
}
ListNode* reverseList(ListNode* prev, ListNode* a, ListNode* b) {
ListNode* cur=a, *nxt;
while (cur != b) {
nxt = cur->next;
cur->next = prev;
prev = cur;
cur = nxt;
}
return prev;
}
};
|
\142. Linked List Cycle II
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *fast = head, *slow = head;
while (fast && fast->next) {
fast = fast->next->next;
slow = slow->next;
if(fast == slow) { // there exits a cycle
ListNode *entry = head;
while (entry != slow) {
entry = entry->next;
slow = slow->next;
}
return entry;
}
}
return nullptr;
}
};
|
\143. Reorder List
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
// 反转后半部分链表,然后重新连接
class Solution {
public:
void reorderList(ListNode* head) {
ListNode *fast=head, *slow=head;
while (fast->next && fast->next->next) { // fast 指向链表最后一个元素,slow指向中间的元素
fast = fast->next->next;
slow = slow->next;
}
// 此时slow 指向=> 3
// 1 -> 2 -> 3 -> 4 -> 5
fast = reverseList(slow); //反转后半部分(即3->4->5)
// => 1->2->3<-4<-5
ListNode *cur = head;
ListNode *left = head->next, *right = fast->next;
while (cur) {
cur->next = fast; // 1->5
cur = left; // cur =>(指向) 2, => 3
if(left) left = left->next;
fast->next = cur; // 5->2
fast = right; // fast => 4, => 3
if(right) right = right->next;
}
}
ListNode* reverseList(ListNode *a) {
ListNode *cur=a, *next, *prev=nullptr;
while (cur != nullptr) {
next = cur->next;
cur->next = prev;
prev = cur;
cur = next;
}
return prev;
}
};
|
\147. Insertion Sort List
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public:
ListNode* insertionSortList(ListNode* head) {
if(!head) return nullptr;
ListNode *dummy = new ListNode(INT_MIN);
ListNode *cur = head; // 将要插入的节点
ListNode *prev=dummy, *next = nullptr;
while (cur) {
next = cur->next;
// 找到一个正确插入的位置
while (prev->next && prev->next->val < cur->val) {
prev = prev->next;
}
// 在prev 与 prev.next中间插入
cur->next = prev->next;
prev->next = cur;
cur = next;
prev = dummy;
}
return dummy->next;
}
};
|
\148. Sort List
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
public:
ListNode* sortList(ListNode* head) {
if(!head || !head->next) return head;
ListNode *fast = head->next, *slow = head;
while (fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
}
fast = slow->next;
slow->next = nullptr; // 从中间切分为两个链表
return mergeSort(sortList(head), sortList(fast));
}
ListNode* mergeSort(ListNode* l1, ListNode* l2) {
ListNode* dummy = new ListNode(0);
ListNode* cur = dummy;
while (l1 && l2) {
if(l1->val < l2->val) {
cur->next = l1;
l1 = l1->next;
} else {
cur->next = l2;
l2 = l2->next;
}
cur = cur->next;
}
cur->next = l1 ? l1 : l2;
return dummy->next;
}
};
|
\382. Linked List Random Node
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
// 参考 水塘抽样:https://www.cnblogs.com/grandyang/p/5759926.html
class Solution {
public:
Solution(ListNode* head) {
this->head = head;
}
int getRandom() {
int res = head->val;
int length = 2, j;
ListNode *cur = head->next;
while (cur) {
j = rand() % length;
if(!j) res = cur->val;
++ length;
cur = cur->next;
}
return res;
}
private:
ListNode *head;
};
|
\445. Add Two Numbers II
分析:方法1:反转链表;方法2:栈 + 尾插法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
// 栈+尾插法 时间复杂度O(max(m, n)) beats 100%, 空间复杂度O(m+n)
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
stack<int> s1, s2;
while (l1) {
s1.push(l1->val);
l1 = l1->next;
}
while (l2) {
s2.push(l2->val);
l2 = l2->next;
}
int carry = 0, sum = 0;
ListNode *dummy = new ListNode(-1);
ListNode *cur = dummy;
// 有一个数还没加完 或者 存在进位
while (!s1.empty() || !s2.empty() || carry>0) {
if(s1.empty()) s1.push(0);
if(s2.empty()) s2.push(0);
int a = s1.top(), b = s2.top();
s1.pop(), s2.pop();
sum = a + b + carry;
// 尾插法
ListNode *node = new ListNode(sum%10);
node->next = cur->next;
cur->next = node;
carry = sum / 10;
}
return dummy->next;
}
};
|
\725. Split Linked List in Parts
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
// time beats 96%, memory beats 9%
class Solution {
public:
vector<ListNode*> splitListToParts(ListNode* head, int k) {
vector<ListNode*> res;
ListNode *cur = head, *pre=head;
int length = 0;
while (cur) {
++ length;
cur = cur->next;
}
while (k) {
int num = ceil(1.0*length/k);
length -= num;
cur = head;
if(!cur) {
while (k--) {
res.push_back(nullptr);
break;
}
continue;
}
k--;
cout<<num<<endl;
for (int i=0; i<num-1; i++) {
if(cur) cur = cur->next;
}
pre = cur->next;
cur->next = nullptr;
res.push_back(head);
head = pre;
}
return res;
}
};
|
\1721. Swapping Nodes in a Linked List
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public:
ListNode* swapNodes(ListNode* head, int k) {
ListNode *fast=head, *slow=head, *node;
while (--k) {
fast = fast->next;
}
node = fast;
fast = fast->next;
while (fast) {
fast = fast->next;
slow = slow->next;
}
swap(node->val, slow->val);
return head;
}
};
|
\817. Linked List Components
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public:
int numComponents(ListNode* head, vector<int>& nums) {
unordered_set<int> s(nums.begin(), nums.end());
int res = 0;
while (head) {
if(s.count(head->val) && (!head->next || !s.count(head->next->val))) res ++;
head = head->next;
}
return res;
}
};
|
\1019. Next Greater Node In Linked List
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
// 最直接的想法:顺序遍历链表节点 找到严格大于该节点的右侧节点值
// 时间复杂度: O(n^2)
class Solution {
public:
vector<int> nextLargerNodes(ListNode* head) {
ListNode *cur = head, *p = head;
vector<int> res;
while (cur) {
while (p && p->val <= cur->val) p = p->next;
if(p && p->val > cur->val) res.push_back(p->val);
else res.push_back(0);
cur = cur->next, p = cur;
}
return res;
}
};
// 维持一个单调栈st, 用于将当前节点元素 与 前面的节点元素值 的比较。 参考:https://www.cnblogs.com/grandyang/p/14383745.html
// 时间复杂度O(n), 空间复杂度O(n)
class Solution {
public:
vector<int> nextLargerNodes(ListNode* head) {
ListNode *cur = head;
vector<int> res;
stack<int> st;
while (cur) {
while (st.size() && res[st.top()] < cur->val) {
res[st.top()] = cur->val;
st.pop();
}
st.push(res.size());
res.push_back(cur->val);
cur = cur->next;
}
while (!st.empty()) {
res[st.top()] = 0;
st.pop();
}
return res;
}
};
|
\1171. Remove Zero Sum Consecutive Nodes from Linked List
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
// 前序和 时间复杂度O(n)
class Solution {
public:
ListNode* removeZeroSumSublists(ListNode* head) {
unordered_map<int, ListNode*> um;
ListNode *dummy = new ListNode(0);
dummy->next = head;
um[0] = dummy;
ListNode *cur = head;
int sum = 0;
while (cur) {
sum += cur->val;
if(um.find(sum) != um.end()) { // 找到连续和为0的子链
ListNode *prev = um[sum], *start = prev;
int xsum = sum;
while (prev != cur) {
prev = prev->next;
xsum += prev->val;
if(prev != cur) um.erase(xsum);
}
start->next = cur->next;
} else {
um[sum] = cur;
}
cur = cur->next;
}
return dummy->next;
}
};
|
\1367. Linked List in Binary Tree
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public:
bool isSubPath(ListNode* head, TreeNode* root) {
if(!root) return false;
return dfs(head, root) || isSubPath(head, root->left) || isSubPath(head, root->right);
}
bool dfs(ListNode* head, TreeNode* root) {
if(!head) return true;
if(!root) return false;
return head->val == root->val && (dfs(head->next, root->left) || dfs(head->next, root->right));
}
};
|
\1669. Merge In Between Linked Lists
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public:
ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {
ListNode *cur = list1, *pre;
b -= (a-1);
while (--a) {
cur = cur->next;
}
pre = cur;
while (b--) {
cur = cur->next;
}
pre->next = list2;
while (list2->next) {
list2 = list2->next;
}
list2->next = cur->next;
return list1;
}
};
|
\2058. Find the Minimum and Maximum Number of Nodes Between Critical Points
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
public:
vector<int> nodesBetweenCriticalPoints(ListNode* head) {
ListNode *prev = nullptr, *cur = head, *next;
int minD = INT_MAX, start=0, end=0;
int length=0;
while (cur) {
++ length;
if(prev && cur->next) {
next = cur->next;
if((prev->val < cur->val && cur->val > next->val)
|| (prev->val > cur->val && cur->val < next->val)) {
if (start) {
minD = min(minD, length-end);
} else {
start = length;
}
end = length;
}
}
prev = cur;
cur = cur->next;
}
if (start == end) {
return vector<int>{-1, -1};
} else {
return vector<int>{minD, end-start};
}
}
};
|
Hard
\23. Merge k Sorted Lists
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
// 1. native idea: 直接将所有列表元素加入到multiset(内部已做了排序),然后尾插法加入结果链表 时间 beats 88%
class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
ListNode* dummy=new ListNode(-1), *prev=dummy;
multiset<int> ms;
for(ListNode* list: lists){
while (list) {
ms.insert(list->val);
list = list->next;
}
}
for(auto iter = begin(ms); iter != end(ms); iter++) {
prev->next = new ListNode(*iter);
prev = prev->next;
}
return dummy->next;
}
};
// 2.用 优先队列, beats 97%
class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
ListNode* dummy=new ListNode(-1), *prev=dummy;
// This comparator will be used to build MIN HEAP.
// We use a LAMBDA to define the comparator.
/*auto comp = [&](ListNode *a, ListNode *b) {
return a->val > b->val;
};
// This priority queue is our MIN HEAP
priority_queue<ListNode *, vector<ListNode *>, decltype(comp)> pq(comp); //decltype() 运行时推导(RTTI)机制,与auto一起用 */
priority_queue<int, vector<int>, greater<int> >pq; // 小顶堆
for(ListNode* list: lists){
while (list) {
pq.push(list->val);
list = list->next;
}
}
while (!pq.empty()) {
prev->next = new ListNode(pq.top());
prev = prev->next;
pq.pop();
}
return dummy->next;
}
};
// 3.分别将n个链表两两比较,节省了空间,但是耗时更多
class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
if(lists.empty()) return nullptr;
ListNode* head = lists[0];
for (int i=1; i<lists.size(); i++)
head = mergeTwoLists(head, lists[i]);
return head;
}
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
if(!l1) return l2;
if(!l2) return l1;
ListNode* head = l1->val < l2->val ? l1 : l2;
ListNode* nohead = l1->val < l2->val ? l2 : l1;
head->next = mergeTwoLists(head->next, nohead);
return head;
}
};
|
\25. Reverse Nodes in k-Group
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
// 头插法+迭代,时间复杂度O(n),空间复杂度O(n).时间 beats 92%
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
ListNode ans(-1);
ListNode *p = head, *res = &ans, *prev; // prev记录反转前的部分(处理不足k个的一组链表)
while (p) {
prev = p;
int num = 0;
ListNode dummy(-1);
ListNode *l = &dummy;
while (p && num++!=k) {
// 头插法
ListNode *node = new ListNode(p->val);
node->next = l->next;
l->next = node;
p = p->next;
}
while (res->next) res = res->next;
if(num < k) {
res->next = prev;
break;
}
else res->next = l->next;
}
return ans.next;
}
};
// 递归 时间 beats 64%,空间 beats 95%。空间复杂度O(n)
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
if(!head) return nullptr;
ListNode* a=head, *b=head;
for(int i=0; i<k; i++) {
if(!b) return head;
b = b->next;
}
ListNode *res = reverseList(a, b);
a->next = reverseKGroup(b, k);
return res;
}
ListNode* reverseList(ListNode* a, ListNode* b) {
ListNode* cur=a, *nxt, *prev = nullptr;
while (cur != b) {
nxt = cur->next;
cur->next = prev;
prev = cur;
cur = nxt;
}
return prev;
}
};
|
Dynamic Programming
Easy
\53. Maximum Subarray
maxSubArray(A, i) = A[i] + (maxSubArray(A, i-1) > 0 ? maxSubArray(A, i-1) : 0);
分析:最大子数列问题,Kadane算法,如下面的方法1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
|
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int sum = 0, res = nums[0];
for (auto x: nums) {
sum += x;
if(res < sum) res = sum;
if(sum < 0) sum = 0;
}
return res;
}
};
// maxSubArray(A, i) = A[i] + (maxSubArray(A, i-1) > 0 ? maxSubArray(A, i-1) : 0);
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int maxSum = nums[0];
vector<int>dp(nums.size());
dp[0] = nums[0];
for (int i=1; i<nums.size(); i++) {
dp[i] = nums[i] + (dp[i-1]>0 ? dp[i-1] : 0);
if (maxSum < dp[i]) maxSum = dp[i];
}
return maxSum;
}
};
// 分治:O(n)
class Solution {
public:
int maxSubArray(vector<int>& nums) {
return maxSubArray(nums, 0, nums.size()-1);
}
int maxSubArray(vector<int> &nums, int l, int r) {
if(l > r) return INT_MIN;
int m = l + (r - l) / 2;
int lmax = maxSubArray(nums, l, m-1);
int rmax = maxSubArray(nums, m+1, r);
int lsum=0, rsum=0;
for (int i = m-1, sum=0; i >= l; i--) {
sum += nums[i];
lsum = max(lsum, sum);
}
for (int i = m+1, sum=0; i <= r; ++i) {
sum += nums[i];
rsum = max(rsum, sum);
}
return max(max(lmax, rmax), lsum+rsum+nums[m]);
}
};
|
\70. Climbing Stairs
1
2
3
4
5
6
7
8
9
10
11
12
13
|
// dp[i] = dp[i-1] + dp[i-2], i in [3, n]
class Solution {
public:
int climbStairs(int n) {
int dp[n+1];
if(n < 3) return n;
dp[1] = 1, dp[2] = 2;
for(int i=3; i<=n; i++) {
dp[i] = dp[i-1] + dp[i-2];
}
return dp[n];
}
};
|
\118. Pascal’s Triangle
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> res;
res.push_back({1}); // 三角形顶部的1
for (int i=1; i<numRows; i++) {
vector<int>dp(res[i-1].begin(), res[i-1].end());
for(int j=i-1; j>0; j--) {
dp[j] = dp[j-1] + dp[j];
}
dp.push_back(1); // 三角形右侧的1
res.push_back(dp);
}
return res;
}
};
|
\119. Pascal’s Triangle II
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public:
vector<int> getRow(int rowIndex) {
if (rowIndex == 0) return vector<int>{1};
vector<vector<int>> res;
res.push_back({1}); // 三角形顶部的1
for (int i=1; i<=rowIndex; i++) {
vector<int>dp(res[i-1].begin(), res[i-1].end());
for(int j=i-1; j>0; j--) {
dp[j] = dp[j-1] + dp[j];
}
dp.push_back(1); // 三角形右侧的1
res.push_back(dp);
}
return res[rowIndex];
}
};
|
\121. Best Time to Buy and Sell Stock
You are given an array prices where prices[i] is the price of a given stock on the ith day.
You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.
Example 1:
1
2
3
4
|
Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
|
Example 2:
1
2
3
|
Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.
|
分析: 改成最大子数列问题。Kadane算法
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public:
int maxProfit(vector<int>& prices) {
int max_so_far = 0, max_ending_here = 0;
for (int i=1; i<prices.size(); i++) {
max_ending_here = max(0, max_ending_here + prices[i] - prices[i-1]);
max_so_far = max(max_so_far, max_ending_here);
}
return max_so_far;
}
};
|
\338. Counting Bits
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
/* 分析:写出前几项分析知,当i==pow(2, k)时,dp[i] = 1,;当pow(2,k+1)>i>pow(2, k)时,dp[i] = dp[i-pow(2,k)] + dp[pow(2,k)]。 代码如下:
*/
class Solution {
public:
vector<int> countBits(int n) {
vector<int>dp(n+1, 0);
if(!n) return vector<int>{0};
dp[0] = 0, dp[1] = 1;
int k=0;
for(int i=1; i<=n; i++) {
int temp = pow(2, k);
if(temp == i) {
k++;
dp[i] = 1;
continue;
}
dp[i] = dp[i-int(pow(2, k-1))] + dp[int(pow(2, k-1))];
}
return dp;
}
};
// 时间复杂度O(n)
// 更简单的,dp[i] = dp[i&(i-1)] + 1
class Solution {
public:
vector<int> countBits(int n) {
vector<int>dp(n+1, 0);
dp[0] = 0;
for(int i=1; i<=n; i++) {
dp[i] = dp[i&(i-1)] + 1;
}
return dp;
}
};
|
\392. Is Subsequence
分析:动态规划,最长公共子序列问题
i = 0 or j =0, dp[i, j] = 0;
i, j > 0, x_i = y_j, dp[i, j] = 1 + dp[i-1, j-1];
i, j > 0, x_i != y_j, dp[i, j] = max(dp[i-1, j], dp[i, j-1]);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
// 双指针
class Solution {
public:
bool isSubsequence(string s, string t) {
int i=0, j=0;
while (s[i] && t[j]) {
if(s[i] == t[j]) i++;
j++;
}
return i == s.length();
}
};
// 动态规划
// 最长公共子序列问题
class Solution {
public:
bool isSubsequence(string s, string t) {
int m = s.length(), n = t.length();
vector<vector<int>> dp(m+1, vector<int>(n+1, 0));
for(int i=0; i<=m; i++) {
dp[i][0] = 0;
}
for(int j=0 ;j<=n; j++) {
dp[0][j] = 0;
}
for(int i=1; i<=m; i++) {
for(int j=1; j<=n; j++) {
if(s[i-1] == t[j-1]) dp[i][j] = 1 + dp[i-1][j-1];
else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
}
}
return dp[m][n] == m;
}
};
|
\746. Min Cost Climbing Stairs
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
/**
* dp[i][0]: 表示不选择cost[i], dp[i][1]表示不选择cost[i]
* 时间复杂度O(n), 空间复杂度O(n*2)
*/
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int sz = cost.size();
int dp[sz][2];
dp[0][0] = INT_MAX, dp[0][1] = cost[0];
dp[1][0] = cost[0], dp[1][1] = cost[1];
for(int i=2; i<cost.size(); i++) {
dp[i][0] = dp[i-1][1];
dp[i][1] = cost[i] + min(dp[i-1][0], dp[i-1][1]);
}
return min(dp[sz-1][0], dp[sz-1][1]);
}
};
// 优化,使用一维数组 beats 100%, 95%. 空间复杂度O(n)
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int sz = cost.size();
int dp[sz];
dp[0] = cost[0], dp[1] = cost[1];
for(int i=2; i<cost.size(); i++) {
dp[i] = cost[i] + min(dp[i-1], dp[i-2]);
}
return min(dp[sz-1], dp[sz-2]);
}
};
// 分析:在上一个方法中,实际上只用到了一维数组中的两个元素,故可以用两个变量来代替.空间复杂度O(1)
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int first, second;
first = cost[0], second = cost[1];
for(int i=2; i<cost.size(); i++) {
int cur = cost[i] + min(first, second);
first = second;
second = cur;
}
return min(first, second);
}
};
|
\509. Fibonacci Number
1
2
3
4
5
6
7
8
9
10
11
12
13
|
class Solution {
public:
int fib(int n) {
if(n < 2) return n;
int first = 0, second = 1;
for(int i=2; i<=n; i++) {
int temp = first + second;
first = second;
second = temp;
}
return second;
}
};
|
Medium
\5. Longest Palindromic Substring
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
|
//扩展中心法
class Solution {
public:
pair<int, int> expand(const string &s, int l, int r) {
while (l>=0 && r<s.size() && s[l] == s[r]) {
l--, r++;
}
return {l+1, r-1};
}
string longestPalindrome(string s) {
int start=0, end=0;
for (int i=0; i<s.size(); i++) {
auto [l1, r1] = expand(s, i, i);
auto [l2, r2] = expand(s, i, i+1);
if(r1 - l1 > end - start) {
start = l1, end = r1;
}
if(r2 - l2 > end - start) {
start = l2, end = r2;
}
}
return s.substr(start, end - start + 1);
}
};
// 马拉车算法,时间复杂度O(n), 空间复杂度O(n)
class Solution {
public:
string preprocess(string s) {
string res(s.size()*2+1, 0);
res[0] += '#';
for (int i=0; i<s.size(); i++) {
res[i*2+1] = s[i];
res[i*2+2] = '#';
}
return res;
}
string longestPalindrome(string s) {
string targetS=preprocess(s);
int len = targetS.length();
vector<int>halfLenArr(len, 0);
int longestHalfLen=0, Center=0;
int rightSide=0;
int rightSideCenter=0; // 右边界和边界中心
for(int i=0; i<len; i++) {
bool needExpand = true;
// 右边界覆盖了当前中心
if (rightSide > i) {
int leftCenter = 2 * rightSideCenter - i;
//根据回文性质得到的结论
halfLenArr[i] = halfLenArr[leftCenter];
if (i + halfLenArr[i] > rightSide) {
//调整当前最长回文子串长度
halfLenArr[i] = rightSide - i;
}
// 可以根据已知条件计算得出最长回文小于右边界,则不需要扩展了
if (i + halfLenArr[leftCenter] < rightSide) {
needExpand = false;
}
}
// 需要中心扩展
if (needExpand) {
while (i-halfLenArr[i]-1 >= 0 && i+halfLenArr[i]+1 < len) {
if (targetS[i-halfLenArr[i]-1] == targetS[i+halfLenArr[i]+1]) {
halfLenArr[i] ++;
} else {
break;
}
}
rightSide = i + halfLenArr[i];
rightSideCenter = i;
if (longestHalfLen < halfLenArr[i]) {
longestHalfLen = halfLenArr[i];
Center = i;
}
}
}
string res="";
for(int i=Center-longestHalfLen+1; i<=Center+longestHalfLen; i+=2) {
res += targetS[i];
}
return res;
}
};
|
\62. Unique Paths
分析:组合数:$C_{n+m-2}^{m-1}, m<=n$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
// 组合数
class Solution {
public:
int uniquePaths(int m, int n) {
if(n < m) swap(m, n); // n >= m
const int maxn = 100 + 5;
int N = n+m-2, M = m-1;
unsigned long long C[maxn][maxn];
for(int i=0; i<maxn; i++) {
C[0][i] = 0;
C[i][0] = 1;
}
for(int i=1; i<maxn; i++) {
for(int j=1; j<maxn; j++) {
C[i][j] = C[i-1][j-1] + C[i-1][j];
}
}
return C[N][M];
}
};
// res = N*...*(N-M+1)/(M*(M-1)*...*1)
class Solution {
public:
int uniquePaths(int m, int n) {
if(n < m) swap(m, n); // n >= m
const int maxn = 100 + 5;
int N = n+m-2, M = m-1;
unsigned long long res = 1;
for(int i=N; i>=(N-M+1); i--) res *= i;
while (M) res /= M, M--;
return res;
}
};
|
\63. Unique Paths II
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int n = obstacleGrid.size(), m = obstacleGrid[0].size();
vector<vector<int> > dp(n+1, vector<int>(m+1, 0));
dp[0][1] = 1;
for (int i=1; i<=n; i++) {
for (int j=1; j<=m; j++) {
dp[i][j] = !obstacleGrid[i-1][j-1] ? (dp[i][j-1] + dp[i-1][j]) : 0;
}
}
return dp[n][m];
}
};
|
\64. Minimum Path Sum
分析:类似于\63. Unique Paths II, 不同的是这里走过的路径不再是1,而是带有权重的。DP思路与63题相似,只需要对 最后一步 是right 还是down的大小进行判断,取多种路径中路径和更小的即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<int>> dp(n+1, vector<int>(m+1, 2e4+5));
dp[1][0] = dp[0][1] = 0;
for (int i=1; i<=n; i++) {
for (int j=1; j<=m; j++) {
int rsum, dsum;
rsum = dp[i][j-1] + grid[i-1][j-1]; // 最后一步是right
dsum = dp[i-1][j] + grid[i-1][j-1]; // 最后一步是down
// 取多种路径中更小的路径和
if (rsum < dp[i][j]) dp[i][j] = rsum;
if (dsum < dp[i][j]) dp[i][j] = dsum;
// cout<<i<<","<<j<<":"<<dp[i][j]<<endl;
}
}
return dp[n][m];
}
};
|
\91. Decode Ways
参考:https://leetcode.com/problems/decode-ways/discuss/30451/Evolve-from-recursion-to-dp
分析如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
// 递归,TLE!!! 时间复杂度O(2^n)
class Solution {
public:
int numDecodings(string s) {
return s.empty() ? 0 : numDecodings(0, s);
}
int numDecodings(int p, string &s) {
int sz = s.size();
if(p == sz) return 1; // 只有最后一个字符
if(s[p] == '0') return 0; // 前导0
int res = numDecodings(p+1, s); // 当前位置p可以解码为合法的单个字符,处理s中的后续字符
if(p < sz-1 && (s[p] == '1' || (s[p] == '2' && s[p+1] < '7'))) // 当前字符与下一个字符解码为一个合法字母
res += numDecodings(p+2, s);
return res;
}
};
// 记忆递归法,beats 100% / 91%。记忆法 起到剪枝效果
class Solution {
public:
int numDecodings(string s) {
int sz = s.size();
vector<int> mem(sz+1, -1);
mem[sz] = 1; // 最后一个字符形成合法串,记为1
return s.empty() ? 0 : numDecodings(0, s, mem);
}
int numDecodings(int p, string &s, vector<int> &mem) {
int sz = s.size();
if(mem[p] > -1) return mem[p]; // 前面计算过[0, p]对应的子串的结果,则直接返回。起到了剪枝效果!
if(s[p] == '0') return mem[p] = 0; // 索引p位置是0,是前导0,不合法
int res = numDecodings(p+1, s, mem); // 当前位置p可以解码为合法的单个字符,处理s中的后续字符
if(p < sz-1 && (s[p] == '1' || (s[p] == '2' && s[p+1] < '7'))) // 当前字符与下一个字符解码为一个合法字母
res += numDecodings(p+2, s, mem);
return mem[p] = res;
}
};
// DP: 时间复杂度O(n),空间复杂度O(n) beats 100% / 41%
// dp[i]: 表示 索引为 区间[i, sz)所解码的合法字符种类
class Solution {
public:
int numDecodings(string s) {
int sz = s.size();
vector<int>dp(sz+1, 0);
dp[sz] = 1; // 最后一个字符是合法字符
for(int i=sz-1; i>=0; i--) {
if(s[i] == '0') dp[i] = 0;
else { // 不存在前导0
dp[i] = dp[i+1];
if(i < sz-1 && (s[i]=='1' || s[i] == '2' && s[i+1] < '7')) dp[i] += dp[i+2];
}
}
return s.empty() ? 0 : dp[0];
}
};
// 实际上只用到了两个int空间,故可以压缩到常量复杂度O(1), beats 100% / 99%
class Solution {
public:
int numDecodings(string s) {
int sz = s.size();
int pp, p = 1;
for(int i=sz-1; i>=0; i--) {
int cur = s[i] == '0' ? 0 : p;
if(i < sz-1 && (s[i]=='1' || s[i] == '2' && s[i+1] < '7')) cur += pp;
pp = p;
p = cur;
}
return s.empty() ? 0 : p;
}
};
|
\97. Interleaving String
\120. Triangle
1
2
3
4
5
6
7
8
9
10
11
12
|
class Solution {
public:
int minimumTotal(vector<vector<int>>& triangle) {
vector<int> dp(triangle.back());
for(int i=triangle.size()-2; i>=0; i--) {
for(int j=0; j<=i; j++) {
dp[j] = triangle[i][j] + min(dp[j], dp[j+1]);
}
}
return dp[0];
}
};
|
\131. Palindrome Partitioning
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
// 回溯,beats 98% / 78%
class Solution {
public:
vector<vector<string>> partition(string s) {
vector<vector<string>> res;
if(s.empty()) return res;
vector<string> temp;
dfs(0, temp, res, s);
return res;
}
void dfs(int index, vector<string> &temp, vector<vector<string>> &res, string &s) {
if(index == s.size()) {
res.push_back(temp);
return;
}
for(int i=index; i<s.size(); i++) {
if(isPalindrome(s, index, i)) { // [index, i]对应的连续子串 构成回文串
temp.push_back(s.substr(index, i - index + 1));
dfs(i + 1, temp, res, s);
temp.pop_back(); // 回溯
}
}
}
bool isPalindrome(const string &s, int start, int end) {
while (start <= end) {
if(s[start++] != s[end--]) return false;
}
return true;
}
};
|
\221. Maximal Square
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
// dp[i][j]: 代表(i,j) 位置能够形成的最大正方形的边长
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int n = matrix.size(), m = matrix[0].size();
vector<vector<int>>dp(n+1, vector<int>(m+1, 0));
int size = 0;
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
if(!i || !j || matrix[i][j] == '0') dp[i][j] = matrix[i][j] - '0';
else {
dp[i][j] = 1 + min(dp[i-1][j-1], min(dp[i-1][j], dp[i][j-1]));
}
if (size < dp[i][j]) size = dp[i][j];
}
}
return size * size;
}
};
// cur[j]: 表示(*, j) 位置能够形成的最大正方形的边长
class Solution {
public:
int maximalSquare(vector<vector<char>>& matrix) {
int n = matrix.size(), m = matrix[0].size();
vector<vector<int>>dp(n+1, vector<int>(m+1, 0));
int size = 0, pre;
vector<int> cur(m, 0);
for(int i=0; i<n; i++) {
for(int j=0; j<m; j++) {
int temp = cur[j];
if(!i || !j || matrix[i][j] == '0') cur[j] = matrix[i][j] - '0';
else {
cur[j] = min(pre, min(cur[j], cur[j-1])) + 1;
}
if (size < cur[j]) size = cur[j];
pre = temp;
}
}
return size * size;
}
};
|
\152. Maximum Product Subarray
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
// 时间复杂度O(n), 空间复杂度O(1)
class Solution {
public:
int maxProduct(vector<int>& nums) {
int max_cur, min_cur, max_so_far, max_cur_pre, min_cur_pre;
max_so_far = max_cur_pre = min_cur_pre = nums[0];
for (int i=1; i<nums.size(); i++) {
min_cur = min(min(min_cur_pre*nums[i], max_cur_pre*nums[i]), nums[i]);
max_cur = max(max(min_cur_pre*nums[i], max_cur_pre*nums[i]), nums[i]);
max_so_far = max(max_so_far, max_cur);
max_cur_pre = max_cur;
min_cur_pre = min_cur;
}
return max_so_far;
}
};
|
\264. Ugly Number II
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
int nthUglyNumber(int n) {
vector<int> v;
int x2=0, x3=0, x5=0;
v.push_back(1);
for(int i=1; i<n; i++) {
int next = min(2*v[x2], min(3*v[x3], 5*v[x5]));
v.push_back(next);
if(next == 2*v[x2]) x2++;
if(next == 3*v[x3]) x3++;
if(next == 5*v[x5]) x5++;
}
for(auto x: v) cout<<x<<" ";
cout<<endl;
cout<<v.back()<<endl;
return v.back();
}
};
|
\309. Best Time to Buy and Sell Stock with Cooldown
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
int maxProfit(vector<int>& prices) {
// buy[i]: 表示在第i天 买入股票时的最大利润,sell[i]:表示在第i天 卖出股票时的最大利润
if(prices.size() < 2) return 0;
int n = prices.size(), res = 0;
vector<int> buy(n);
vector<int> sell(n);
buy[0] = -prices[0];
for(int i=1; i<n; i++) {
// sell[i] = 第i-1天没卖出但在第i天卖出 与 第i-1天买入但在第i天卖出 两者之间的最大值
sell[i] = max(sell[i-1]-prices[i-1] + prices[i], buy[i-1] + prices[i]);
if(sell[i] > res) res = sell[i];
if(i == 1) buy[i] = buy[0] + prices[0] - prices[1];
else buy[i] = max(sell[i-2] - prices[i], buy[i-1] + prices[i-1] - prices[i]);
}
return res;
}
};
|
\313. Super Ugly Number
- Ugly Number的扩展。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public:
int nthSuperUglyNumber(int n, vector<int>& primes) {
vector<int> nums(primes.size(), 0);
vector<int>v;
v.push_back(1);
for (int k=1; k<n; k++) {
int next, temp;
next = primes[0] * v[nums[0]];
for (int i=1; i<primes.size(); i++) {
if(primes[i] * v[nums[i]] < next) next = primes[i] * v[nums[i]];
}
v.push_back(next);
for (int i=0; i<primes.size(); i++) {
if(next == primes[i] * v[nums[i]]) // 当前数组v中素数primes[i]作为因子的数量+1
nums[i] ++;
}
}
return v[n-1];
}
};
|
\322. Coin Change
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount+1, INT_MAX); // dp[i]: 表示i元钱 最少可以换几张coin
dp[0] = 0;
std::sort(coins.begin(), coins.end());
for(int i=1; i<=amount; i++) { // 枚举剩余的零钱
for(int x: coins) {
if(i - x < 0) break;
if(dp[i-x] != INT_MAX) {
dp[i] = min(dp[i], 1 + dp[i-x]);
}
}
}
return dp[amount] == INT_MAX ? -1 : dp[amount];
}
};
|
\416. Partition Equal Subset Sum
分析:传统0-1背包问题是 不超过背包重量,这里是 恰好等于数组元素和的一般。 类似0-1背包问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
for (auto x: nums) sum += x;
// 和为奇数 一定不能分成两个子集合
if(sum & 1) return false;
int n = nums.size();
bool dp[n+1][sum/2+1];
memset(dp, false, sizeof(dp));
//for (int i=0; i<n; i++) dp[i][0] = true;
dp[0][0] = true; // 数组为空,则一定为true; dp[0][j]表示不选择任何元素, dp[i][j] 表示考虑前i-1个元素
for (int i=1; i<=n; i++) {
for (int j=0; j<=sum/2; j++) {
bool no = dp[i-1][j]; // 不选择当前元素
bool yes = j >= nums[i-1] ? dp[i-1][j-nums[i-1]] : 0; //选择当前元素
dp[i][j] = yes | no;// 只可能有一个
}
}
return dp[n][sum/2];
}
};
// 滚动数组
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
for (auto x: nums) sum += x;
// 和为奇数 一定不能分成两个子集合
if(sum & 1) return false;
int n = nums.size();
bool dp[2][sum/2+1];
memset(dp, false, sizeof(dp));
dp[0][0] = true; // 数组为空,则一定为true; dp[0][j]表示不选择任何元素, dp[i][j] 表示考虑前i-1个元素
for (int i=1; i<=n; i++) {
for (int j=0; j<=sum/2; j++) {
bool no = dp[(i-1)&1][j]; // 不选择当前元素
bool yes = j >= nums[i-1] ? dp[(i-1)&1][j-nums[i-1]] : 0; //选择当前元素
dp[i&1][j] = yes | no;
}
}
return dp[n&1][sum/2];
}
};
// 一维空间优化
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
for (auto x: nums) sum += x;
// 和为奇数 一定不能分成两个子集合
if(sum & 1) return false;
int n = nums.size();
bool dp[sum/2+1];
memset(dp, false, sizeof(dp));
dp[0] = true; // 数组为空,则一定为true; dp[0][j]表示不选择任何元素, dp[i][j] 表示考虑前i-1个元素
for (int i=1; i<=n; i++) {
for (int j=sum/2; j>=0; j--) {
bool no = dp[j]; // 不选择当前元素
bool yes = j >= nums[i-1] ? dp[j-nums[i-1]] : 0; //选择当前元素
dp[j] = yes | no;
}
}
return dp[sum/2];
}
};
|
\464. Can I Win
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
class Solution {
public:
bool canIWin(int maxChoosableInteger, int desiredTotal) {
int sum = maxChoosableInteger * (maxChoosableInteger + 1) / 2;
if (maxChoosableInteger >= desiredTotal) return true;
if (sum < desiredTotal) return false;
if (sum == desiredTotal) return maxChoosableInteger % 2; // 奇数个数,则先手获胜;否则后手胜
unordered_map<int, bool> m;
return dfs(maxChoosableInteger, desiredTotal, 0, m);
}
bool dfs(int M, int T, int k, unordered_map<int, bool> &m) {
/**
* M : 表示最大可选择的整数
* T : 表示目标整数和
* k : 表示当前游戏的状态
* m : 表示当前游戏胜负状态, true 表示 先手胜, false 表示后手胜
*/
if (T <= 0) return false;
if (m.count(k)) return m[k];
for (int i=0; i<M; i++) {
// 如果(i+1)是可选的,我选后我的对手不能赢,我赢!
if(!(k & 1<<i) && !dfs(M, T-i-1, k|1<<i, m)) {
return m[k] = true;
}
}
return m[k] = false;
}
};
// 使用数组优化
class Solution {
public:
bool canIWin(int maxChoosableInteger, int desiredTotal) {
int sum = maxChoosableInteger * (maxChoosableInteger + 1) / 2;
if (maxChoosableInteger >= desiredTotal) return true;
if (sum < desiredTotal) return false;
if (sum == desiredTotal) return maxChoosableInteger % 2; // 奇数个数,则先手获胜;否则后手胜
return dfs(maxChoosableInteger, desiredTotal, 0);
}
bool dfs(int M, int T, int k) {
/**
* M : 表示最大可选择的整数
* T : 表示目标整数和
* k : 表示当前游戏的状态
* m : 表示当前游戏胜负状态, true 表示 先手胜, false 表示后手胜
*/
if (T <= 0) return false;
if (m[k]) return m[k] > 0;
for (int i=0; i<M; i++) {
// 如果(i+1)是可选的,我选后我的对手不能赢,我赢!
if(!(k & 1<<i) && !dfs(M, T-i-1, k|1<<i)) {
return (m[k] = 1) > 0;
}
}
return m[k] = 0;
}
private:
int m[1<<20] = {0};
};
|
\474. Ones and Zeroes
分析:典型的背包问题。 01背包
dp[i][j][k]: 表示前i个字符串中,至多j个0 k个1 的最大子串集合的最大数量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
int sz = strs.size();
int dp[sz+1][m+1][n+1];
// dp[i][j][k]: 表示前i个字符串中,至多j个0 k个1 的最大子串集合的最大数量
memset(dp, 0, sizeof(dp));
for(int i=1; i<=sz; i++) {
int num_ones = count(strs[i-1].begin(), strs[i-1].end(), '1');
int num_zeroes = strs[i-1].size() - num_ones;
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= n; k++) {
if(j >= num_zeroes && k >= num_ones) // 剩余的j k要比当前串的0 1数量多,即 放得下
dp[i][j][k] = max(dp[i-1][j][k], 1 + dp[i-1][j-num_zeroes][k-num_ones]);
else
dp[i][j][k] = dp[i-1][j][k];
}
}
}
return dp[sz][m][n];
}
};
// 观察发现第一维可以压缩。
// !!! 必须从右下角往左上角遍历! 保证dp[i]是从dp[i-1]转移得到的
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
int sz = strs.size();
int dp[m+1][n+1];
// dp[i][j][k]: 表示前i个字符串中,至多j个0 k个1 的最大子串集合的最大数量
memset(dp, 0, sizeof(dp));
for(int i=1; i<=sz; i++) {
int num_ones = count(strs[i-1].begin(), strs[i-1].end(), '1');
int num_zeroes = strs[i-1].size() - num_ones;
for (int j = m; j>=num_zeroes; j--) {
for (int k = n; k>=num_ones; k--) {
dp[j][k] = max(dp[j][k], 1 + dp[j-num_zeroes][k-num_ones]);
}
}
}
return dp[m][n];
}
};
|
\486. Predict the Winner
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
|
// 递归
class Solution {
public:
bool PredictTheWinner(vector<int>& nums) {
int scoreFirst = dfs(nums, 0, nums.size()-1);
int scoreTotal = 0;
for (auto x: nums) scoreTotal += x;
return scoreFirst >= scoreTotal - scoreFirst;
}
int dfs(vector<int> &nums, int l, int r) {
if(l > r) return 0;
if(l == r) return nums[l];
int curScore = max(nums[l] + min(dfs(nums, l+2, r), dfs(nums, l+1, r-1)),
nums[r] + min(dfs(nums, l+1, r-1), dfs(nums, l, r-2)));
return curScore;
}
};
// 记忆化,自顶向下
class Solution {
public:
bool PredictTheWinner(vector<int>& nums) {
vector<vector<int>> mem(nums.size(), vector<int>(nums.size(), -1));
int scoreFirst = dfs(nums, 0, nums.size()-1, mem);
int scoreTotal = 0;
for (auto x: nums) scoreTotal += x;
return scoreFirst >= scoreTotal - scoreFirst;
}
int dfs(vector<int> &nums, int l, int r, vector<vector<int>>&mem) {
if (l > r) return 0;
if (l == r) return nums[l];
if(mem[l][r] != -1) return mem[l][r];
int curScore = max(nums[l] + min(dfs(nums, l + 2, r, mem), dfs(nums, l + 1, r - 1, mem)),
nums[r] + min(dfs(nums, l + 1, r - 1, mem), dfs(nums, l, r - 2, mem)));
return mem[l][r] = curScore;
}
};
// DP 自底向上
class Solution {
public:
bool PredictTheWinner(vector<int>& nums) {
int n = nums.size();
vector<vector<int>> dp(n, vector<int>(n, 0)); //dp[i][j] 表示first player 在nums[i...j]选择元素的最大和
int scoreTotal = 0;
for (auto x: nums) scoreTotal += x;
for (int len = 1; len <= n; len++) { // 枚举长度
for (int i=0; i <= n-len; i++) { // 枚举左边界
int j = i + len - 1; // 右边界
/** first player 选择 nums[i]时,
* second player 选择nums[i+1](最大化), 则first player在nums[(i+2)...j] 里面选择
选择nums[j](最大化), nums[(i+1)...(j-1)]
* first player 选择nums[j]时,
* second player 选择nums[i](最大化), 则first player 在nums[(i+1)...(j-1)]里面选择
* 选择nums[j-1](最大化), nums[i...(j-2)]
*/
int a = (i + 1 < n && j - 1 >= 0) ? dp[i+1][j-1] : 0;
int b = (i + 2 < n) ? dp[i+2][j] : 0;
int c = (j - 2 >= 0) ? dp[i][j-2] : 0;
dp[i][j] = max(nums[i] + min(a, b), nums[j] + min(a, c));
}
}
int scoreFirst = dp[0][n-1];
return scoreFirst >= scoreTotal - scoreFirst;
}
};
|
\494. Target Sum
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
|
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int res = 0;
dfs(res, nums, 0, 0, target);
return res;
}
void dfs(int &res, vector<int>& nums, int index, int sum, int &target) {
if(index >= nums.size()) {
if (sum == target) res ++;
return ;
}
dfs(res, nums, index+1, sum+nums[index], target);
dfs(res, nums, index+1, sum-nums[index], target);
}
};
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int res = 0;
dfs(res, nums, 0, target);
return res;
}
void dfs(int &res, vector<int>& nums, int index, int target) {
if(index >= nums.size()) {
if (0 == target) res ++;
return ;
}
dfs(res, nums, index+1, target-nums[index]);
dfs(res, nums, index+1, target+nums[index]);
}
};
// 记忆递归法
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
map<string, int>mp;
return dfs(nums, 0, target, mp);
}
int dfs(vector<int>& nums, int index, int target, map<string, int>&mp) {
if(index >= nums.size()) {
if (0 == target) return 1;
return 0;
}
string key = to_string(index) + ";" + to_string(target);
if(mp.find(key) != mp.end()) return mp[key];
int res = dfs(nums, index+1, target-nums[index], mp) +
dfs(nums, index+1, target+nums[index], mp);
mp[key] = res;
return res;
}
};
// 动归. 类比698. Partition to K Equal Sum Subsets
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for(auto x: nums) sum += x;
if (sum < target || (sum + target) % 2 == 1) {
// 两种不合法的情况
return 0;
}
return subsets(nums, (sum + target) / 2);
}
// dp[i][j]: 表示前i个元素 和为j的方案数
int subsets(vector<int> &nums, int sum) {
if(sum < 0) sum = -sum; // sum可能是负数
int n = nums.size();
vector<vector<int>>dp(n+1, vector<int>(sum+1, 0));
for(int i=0; i<=n; i++) dp[i][0] = 1;
for(int i=1; i<=n; i++) {
for(int j=0; j<=sum; j++) {
if(j >= nums[i-1]) // 不装第i个物品, 与 装第i个物品
dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i-1]];
else
dp[i][j] = dp[i-1][j]; // 背包的空间不足,选择不装
}
}
return dp[n][sum];
}
};
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for(auto x: nums) sum += x;
if (sum < target || (sum + target) % 2 == 1) {
// 两种不合法的情况
return 0;
}
return subsets(nums, (sum + target) / 2);
}
// dp[i][j]: 表示前i个元素 和为j的方案数
int subsets(vector<int> &nums, int sum) {
if(sum < 0) sum = -sum; // sum可能是负数
int n = nums.size();
int dp[sum + 1];
for (int i=0; i<=sum; i++) dp[i] = 0;
dp[0] = 1;
for(int i=1; i<=n; i++) {
for(int j=sum; j>=nums[i-1]; j--) {
dp[j] = dp[j] + dp[j-nums[i-1]];
}
}
return dp[sum];
}
};
|
\516. Longest Palindromic Subsequence
分析: dp[i][j] : 表示 s[i…j] 最长回文子序列的长度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
class Solution {
public:
int longestPalindromeSubseq(string s) {
int n = s.size();
vector<vector<int>> dp(n, vector<int>(n, 0));
for (int i=0; i<n; i++) dp[i][i] = 1;
for (int i=n-1; i>=0; i--) { // 遍历方向 是反向:由状态转移公式决定的
for (int j=i+1; j<n; j++) {
if(s[i] == s[j]) dp[i][j] = dp[i+1][j-1] + 2;
else dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
}
}
return dp[0][n-1];
}
};
|
\518. Coin Change 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
class Solution {
public:
int change(int amount, vector<int>& coins) {
int n = coins.size();
// dp[i][j] 表示只使用前i个物品(可重复使用),当背包容量为j时 的方法数量可以装满背包
vector<vector<int>> dp(n+1, vector<int>(amount+1, 0));
for(int i=0; i<=n; i++) dp[i][0] = 1;
for (int i=1; i<=n; i++) {
for (int j=1; j<=amount; j++) {
if(j >= coins[i-1]) dp[i][j] = dp[i-1][j] + dp[i][j-coins[i-1]];
else dp[i][j] = dp[i-1][j]; // 背包容量放不下
}
}
return dp[n][amount];
}
};
// O(n*amount) / O(amount)
class Solution {
public:
int change(int amount, vector<int>& coins) {
int n = coins.size();
// dp[j]表示只使用前i个物品(可重复使用),当背包容量为j时 的方法数量可以装满背包
vector<int> dp(amount+1, 0);
dp[0] = 1;
for (int i=1; i<=n; i++) {
for (int j=1; j<=amount; j++) {
if(j>=coins[i-1])
dp[j] = dp[j] + dp[j-coins[i-1]];
}
}
return dp[amount];
}
};
|
\542. 01 Matrix
传送门
Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.
The distance between two adjacent cells is 1.
Example 1:
1
2
|
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]
|
Example 2:
1
2
|
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]
|
Constraints:
m == mat.lengthn == mat[i].length1 <= m, n <= 1041 <= m * n <= 104mat[i][j] is either 0 or 1.- There is at least one
0 in mat.
分析: $m * n <= 10 ^4$,二维数组DP理论上可行。
DP三步走: DP定义;状态转移;初始状态
第一遍扫描左上角(左边和上边):dp[i][j]:表示mat[0, …, i][0, …, j]中每个位置距离最近的0的最小距离
第二遍扫描右上角(右边和下边): dp即为所求
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
int m = mat.size(), n = mat[0].size();
vector<vector<int>>dp(m, vector<int>(n, INT_MAX-1e4)); // 这里减掉1e4 避免后面int类型溢出。
for (int i=0; i<m; i++) {
for (int j=0; j<n; j++) {
if (mat[i][j] == 0) dp[i][j] = 0;
else {
if (i > 0) dp[i][j] = min(dp[i][j], dp[i-1][j] + 1);
if (j > 0) dp[i][j] = min(dp[i][j], dp[i][j-1] + 1);
}
}
}
for (int i=m-1; i>=0; i--) {
for (int j=n-1; j>=0; j--) {
if (i < m-1) dp[i][j] = min(dp[i][j], dp[i+1][j] + 1);
if (j < n-1) dp[i][j] = min(dp[i][j], dp[i][j+1] + 1);
}
}
return dp;
}
};
|
\583. Delete Operation for Two Strings
传送门
分析:将word1转化为word2,每一步可以对任何一个字符串的字符做删除操作,求最少操作步数。
这跟Edit Distance 这道题的简单版。
dp[i][j]:表示word1[0, …, i] 前i个字符转化为word2[0, …, j] 前j个字符所需的最少操作步数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
// DP,自底向上,时间复杂度O(n*m) 空间复杂度O(n*m) beats 99.4% / 92.6%
class Solution {
public:
int minDistance(string word1, string word2) {
int n = word1.size(), m = word2.size();
int dp[n+1][m+1];
for (int i=0; i<=n; i++) dp[i][0] = i;
for (int j=0; j<=m; j++) dp[0][j] = j;
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++) {
if (word1[i] == word2[j]) dp[i+1][j+1] = dp[i][j]; //
else dp[i+1][j+1] = min(dp[i+1][j], dp[i][j+1]) + 1;
}
}
return dp[n][m];
}
};
// 自顶向下
class Solution {
public:
int minDistance(string word1, string word2) {
int n = word1.size(), m = word2.size();
vector<vector<int>>dp (n+1, vector<int>(m+1, -1));
return getMinDistance(n, m, word1, word2, dp);
}
int getMinDistance(int i, int j, string& word1, string& word2, vector<vector<int>>& dp) {
if (i == 0) return dp[0][j] = j;
if (j == 0) return dp[i][0] = i;
if (dp[i][j] != -1) return dp[i][j];
if(word1[i-1] == word2[j-1]) dp[i][j] = getMinDistance(i-1, j-1, word1, word2, dp);
else dp[i][j] = 1 + min(getMinDistance(i-1, j, word1, word2, dp),
getMinDistance(i, j-1, word1, word2, dp));
return dp[i][j];
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
// 类似最长公共子序列
class Solution {
public:
int findLongestChain(vector<vector<int>>& pairs) {
if(pairs.empty()) return 0;
sort(pairs.begin(), pairs.end());
vector<int> lst(pairs.size(), 1);
int longestChainNum = 1;
for(int i=1; i<pairs.size(); i++) {
for(int j=0; j<i; j++) {
if((pairs[j][1] < pairs[i][0]) && (lst[i] < lst[j] + 1)) {
lst[i] = lst[j] + 1;
longestChainNum = max(longestChainNum, lst[i]);
}
}
}
return longestChainNum;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution {
public:
int countSubstrings(string s) {
int res = 0;
for(int i=0; i<s.length(); i++) {
expandAroundCenter(s, i, i+1, res);
expandAroundCenter(s, i, i, res);
}
return res;
}
bool expandAroundCenter(string s, int l, int r, int &res) {
if(s.length() == 0 || l > r) return 0;
while(l>=0 && r<s.length() && s[l] == s[r]) {
l--, r++;
res++;
}
return res;
}
};
|
\698. Partition to K Equal Sum Subsets
分析:递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
bool canPartitionKSubsets(vector<int>& nums, int k) {
int sum = 0;
for(auto x: nums) sum += x;
if(sum % k) return false;
vector<bool> used(nums.size());
int target = sum / k;
return dfs(k, 0, nums, used, target, 0);
}
bool dfs(int k, int index, vector<int> &nums, vector<bool> &used, int target, int sum) {
if(!k) return true;
if(target == sum) {
return dfs(k-1, 0, nums, used, target, 0);
}
for (int i=index; i<nums.size(); i++) {
if(used[i]) continue;
if(target < sum + nums[i]) continue;
used[i] = true;
if(dfs(k, i+1, nums, used, target, sum+nums[i]) == true) {
return true;
}
used[i] = false;
}
return false;
}
};
|
Hard
\42. Trapping Rain Water
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
class Solution {
public:
int trap(vector<int>& height) {
// height[0,i] 表示[0, i)区间的最高高度,height[i+1, n] 表示[i+1, n)区间的最高高度
int n = height.size();
vector<int> h_l(n+1, 0), h_r(n+1, 0);
for (int i=1; i<=n; i++) {
h_l[i] = max(h_l[i-1], height[i-1]);
}
for (int i=n-1; i>=0; i--) {
h_r[i] = max(h_r[i+1], height[i]);
}
int res = 0;
for (int i=1; i<=n; i++) {
res += min(h_l[i], h_r[i-1]) - height[i-1];
}
return res;
}
};
class Solution {
public:
int trap(vector<int>& height) {
// height[0,i] 表示[0, i)区间的最高高度,height[i+1, n] 表示[i+1, n)区间的最高高度
int n = height.size();
vector<int> h_l(n+1, 0), h_r(n+1, 0);
for (int i=1; i<=n; i++) {
h_l[i] = max(h_l[i-1], height[i-1]);
h_r[n-i] = max(h_r[n-i+1], height[n-i]);
}
int res = 0;
for (int i=1; i<=n; i++) {
res += min(h_l[i], h_r[i-1]) - height[i-1];
}
return res;
}
};
// 双指针
class Solution {
public:
int trap(vector<int>& height) {
// height[0,i] 表示[0, i)区间的最高高度,height[i+1, n] 表示[i+1, n)区间的最高高度
int n = height.size(), res = 0;
int left = 0, right = n-1, l_max = height[0], r_max = height[n-1];
while (left <= right) {
if(l_max < height[left]) l_max = height[left];
if(r_max < height[right]) r_max = height[right];
if(l_max < r_max) {
res += min(l_max, r_max) - height[left];
left ++;
} else {
res += min(l_max, r_max) - height[right];
right --;
}
}
return res;
}
};
|
\72. Edit Distance
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
// 记忆递归法 自顶向下
class Solution {
public:
int minDistance(string word1, string word2) {
int n = word1.size(), m = word2.size();
vector<vector<int>> dp(n+1, vector<int>(m+1, -1));
return minDistance(n, m, word1, word2, dp);
}
int minDistance(int i, int j, string &s1, string &s2, vector<vector<int>>&dp) {
if (i == 0) return dp[0][j] = j;
if (j == 0) return dp[i][0] = i;
if(dp[i][j] != -1) return dp[i][j];
if(s1[i-1] == s2[j-1]) {
dp[i][j] = minDistance(i-1, j-1, s1, s2, dp); // skip
} else {
dp[i][j] = 1 + min(minDistance(i, j-1, s1, s2, dp), //在s1中插入一个字符
min(minDistance(i-1, j, s1, s2, dp), //在s2中删除一个字符
minDistance(i-1, j-1, s1, s2, dp))); // 在s1中替换一个字符
}
return dp[i][j];
}
};
// 动态规划 自底向上
class Solution {
public:
int minDistance(string word1, string word2) {
int n = word1.size(), m = word2.size();
vector<vector<int>> dp(n+1, vector<int>(m+1, 0));
for (int i=0; i<=n; i++) dp[i][0] = i;
for (int j=0; j<=m; j++) dp[0][j] = j;
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++) {
if(word1[i] == word2[j]) dp[i+1][j+1] = dp[i][j];
else {
dp[i+1][j+1] = min(dp[i][j+1], min(dp[i+1][j], dp[i][j])) + 1;
}
}
}
return dp[n][m];
}
};
|
\132. Palindrome Partitioning II
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
// 记忆回溯法
class Solution {
public:
int minCut(string s) {
int sz = s.size();
vector<vector<int>> dp(sz+1, vector<int>(sz+1, -1));
return dfs(dp, 0, sz-1, s);
}
int dfs(vector<vector<int>> &dp, int i, int j, string &s) {
if(i >= j || isPalindrome(s, i, j)) return 0;
if(dp[i][j] != -1) return dp[i][j];
int ans = INT_MAX;
for(int k=i; k<j; k++) {
if (isPalindrome(s, i, k)) {
// 当[i, k]构成的子串是回文串时
ans = min(ans, 1 + dfs(dp, k+1, j, s));
}
}
return dp[i][j] = ans;
}
bool isPalindrome(const string &s, int start, int end) {
while (start <= end) {
if(s[start++] != s[end--]) return false;
}
return true;
}
};
// 中心,DP 最坏O(n^2)。beats 98% / 94%
class Solution {
public:
int minCut(string s) {
int sz = s.size();
vector<int> dp(sz, 0);
for(int i=0; i<sz; i++) // s[0,i] 至多需要i次切分 得到的子串都是回文串
dp[i] = i;
for(int center=0; center<sz; center++) {
int l, r; // l,r 表示以center为中心的回文串左右边界索引值
// 回文串长度为奇数
l = r = center;
while (l >= 0 && r < sz && s[l] == s[r]) {
dp[r] = min(dp[r], l-1 < 0 ? 0 : (1 + dp[l-1]));
l--, r++;
}
// 回文串长度为偶数
l = center, r = center + 1;
while (l >= 0 && r < sz && s[l] == s[r]) {
dp[r] = min(dp[r], l-1 < 0 ? 0 : (1 + dp[l-1]));
l--, r++;
}
}
return dp[sz-1];
}
};
|
参考:https://leetcode-cn.com/problems/k-inverse-pairs-array/solution/gong-shui-san-xie-yi-dao-xu-lie-dp-zhuan-tm01/
动态规划公式:$f[i][j] = \sum _{k=0}^{i-1}f[i-1][j-k]$. f[i][j]表示[1,…, i]组成k个逆序对的数量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution {
public:
int mod = int(1e9+7);
int kInversePairs(int n, int k) {
int f[n+1][k+1];
int sum[n+1][k+1];
f[1][0] = 1;
for(int j=0; j<=k; j++) sum[1][j] = 1;
for(int i=2; i<=n; i++) {
for (int j=0; j<=k; j++) {
f[i][j] = (j<i ? sum[i-1][j] : (sum[i-1][j] - sum[i-1][j-(i-1)-1]+mod)%mod);
sum[i][j] = (j==0) ? f[i][j] : (sum[i][j-1] + f[i][j]) % mod;
}
}
return f[n][k];
}
};
|
DFS
Medium
\130. Surrounded Regions
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
|
class Solution {
public:
void solve(vector<vector<char>>& board) {
int n = board.size(), m = board[0].size();
for (int i=0; i<n; i++) {
dfs(board, i, 0, 1, 0);
dfs(board, i, m-1, 1, 0);
}
for (int j=0; j<m; j++) {
dfs(board, 0, j, 1, 0);
dfs(board, n-1, j, 1, 0);
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (board[i][j] == 'O') {
dfs(board, i, j, 0, 0);
}
}
}
for (int i=0; i<n; i++) {
dfs(board, i, 0, 1, 1);
dfs(board, i, m-1, 1, 1);
}
for (int j=0; j<m; j++) {
dfs(board, 0, j, 1, 1);
dfs(board, n-1, j, 1, 1);
}
}
void dfs(vector<vector<char>> &board, int i, int j, bool isBoarder, bool flag) {
if(i < 0 || i >= board.size() || j < 0 || j >= board[i].size()) return;
if (board[i][j] == 'X') return;
if (board[i][j] == '#') {
if(flag) board[i][j] = 'O'; // 恢复为'O'
else return; // 已经由 'O'改成的'#'
}
else if(board[i][j] == 'O') {
if(isBoarder && !flag) board[i][j] = '#'; //对边界上的字符'O' 改成'#'作为特殊标记,之后再改回'O'
else if(!isBoarder && !flag) board[i][j] = 'X'; // 四周包围的'O'改成'X'
else return; // 当前字符是'O'的不需要对周边字符修改
}
dfs(board, i, j-1, isBoarder, flag);
dfs(board, i-1, j, isBoarder, flag);
dfs(board, i+1, j, isBoarder, flag);
dfs(board, i, j+1, isBoarder, flag);
}
};
// 并查集
class UnionFind {
private:
/**
* count: 记录连通分量的个数
* parent[i]: 记录节点i的父节点
* size[i]: 记录树i的 “重要”(即整棵树的节点数量)
*/
int count;
vector<int> parent;
vector<int> size;
public:
UnionFind(int n) {
count = n;
parent = vector<int>(n, 0);
size = vector<int>(n, 0);
for (int i=0; i<n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// 将 p, q 连通
void merge(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
// 小树接在大树下面, 这样比较平衡
if (size[rootP] > size[rootQ]) {
size[rootP] += size[rootQ];
parent[rootQ] = parent[rootP];
} else {
size[rootQ] += size[rootP];
parent[rootP] = parent[rootQ];
}
count --;
}
// 查询x的根并做路径压缩
int find(int x) {
while (parent[x] != x) {
parent[x] = parent[parent[x]]; // 压缩路径
x = parent[x];
}
return x;
}
bool connected(int p, int q) {
return find(p) == find(q); // p 与 q的根节点相同则说明p q相互连通
}
};
class Solution {
public:
void solve(vector<vector<char>>& board) {
int n = board.size(), m = board[0].size();
if (!n) return;
UnionFind uf = UnionFind(n * m + 1);
int dummy = n * m;
for (int i=0; i<n; i++) {
// 将首列和末列的O 与 dummy连通
if(board[i][0] == 'O') uf.merge(i*m, dummy);
if(board[i][m-1] == 'O') uf.merge(i*m+m-1, dummy);
}
for (int j=0; j<m; j++) {
// 将首行和末行的O 与 dummy连通
if(board[0][j] == 'O') uf.merge(j, dummy);
if(board[n-1][j] == 'O') uf.merge(m*(n-1)+j, dummy);
}
int d[4][2]={{1,0}, {0,1}, {-1,0}, {0,-1}};
for (int i=1; i<n-1; i++) {
for (int j=1; j<m-1; j++) {
if(board[i][j]=='O') {
// 将 'O' 与 周围的O连通
for (int k=0; k<4; k++) {
int x = i + d[k][0], y= j + d[k][1];
if(board[x][y] == 'O')
uf.merge(x * m + y, i * m + j);
}
}
}
}
// 所有不和dummy连通的O 都要被替换为X
for (int i=1; i<n; i++) {
for (int j=1; j<m; j++) {
if (!uf.connected(dummy, i * m +j)) {
board[i][j] = 'X';
}
}
}
}
};
|
\200. Number of Islands
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
class Solution {
public:
int numIslands(vector<vector<char>>& grid) {
int res = 0;
int n = grid.size(), m = grid[0].size();
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++) {
if (grid[i][j] == '1') {
++ res;
dfs (grid, i, j);
}
}
}
return res;
}
void dfs(vector<vector<char>> &grid, int i, int j) {
if(i < 0 || i >= grid.size() || j < 0 || j >= grid[0].size()) // 越界
return;
if (grid[i][j] == '0') /// 已经是water
return;
grid[i][j] = '0'; // 将岛屿内的'1' 改为'0'
dfs(grid, i-1, j);
dfs(grid, i, j-1);
dfs(grid, i+1, j);
dfs(grid, i, j+1);
}
};
|
\1020. Number of Enclaves
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution {
public:
int numEnclaves(vector<vector<int>>& grid) {
for (int i=0; i<grid.size(); i++) {
for (int j=0; j<grid[0].size(); j++) {
if(!i || !j || i == grid.size()-1 || j == grid[i].size()-1) {
dfs(grid, i, j);
}
}
}
return accumulate(begin(grid), end(grid), 0,
[](int a, vector<int>&v){ return a + accumulate(begin(v), end(v), 0);}
);
}
void dfs(vector<vector<int>> &grid, int i, int j) {
if(i < 0 || i == grid.size() || j < 0 || j == grid[i].size()) return;
if(grid[i][j] != 1) return;
grid[i][j] = 0;
dfs(grid, i-1, j);
dfs(grid, i, j-1);
dfs(grid, i+1, j);
dfs(grid, i, j+1);
}
};
|
\1254. Number of Closed Islands
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
class Solution {
public:
int closedIsland(vector<vector<int>>& grid) {
int n = grid.size(), m = grid[0].size();
for (int i=0; i<n; i++) {
dfs(grid, i, 0);
dfs(grid, i, m-1);
}
for (int j=0; j<m; j++) {
dfs(grid, 0, j);
dfs(grid, n-1, j);
}
int res = 0;
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++) {
if(grid[i][j] == 0) { // 是岛屿
++ res;
dfs(grid, i, j);
}
}
}
return res;
}
void dfs(vector<vector<int>> &grid, int i, int j) {
if(i < 0 || i >= grid.size() || j < 0 || j >= grid[0].size()) return;
if (grid[i][j] == 1) return;
grid[i][j] = 1; // 变成水
dfs(grid, i-1, j);
dfs(grid, i, j-1);
dfs(grid, i+1, j);
dfs(grid, i, j+1);
}
};
|
Union-Find
Easy
Medium
\399. Evaluate Division
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
|
class Solution {
public:
struct Node {
string root; // 根节点
double val; // 根节点的值
Node() {}
Node(string _root, double _val): root(_root), val(_val) {}
};
unordered_map<string, Node> u;
unordered_map<string, int> rank;
string findRoot(string x) {
while (u[x].root != x) {
// 找根
u[x].val = u[x].val * u[u[x].root].val;
u[x].root = u[u[x].root].root; // 压缩路径
x = u[x].root;
}
return x;
}
void unionRoot(string x, string y, double val) {
string rootX = findRoot(x);
string rootY = findRoot(y);
if(rootX == rootY) return;
if(rank[rootX] > rank[rootY]) {
rank[rootX] += rank[rootY];
u[rootY].root = rootX;
u[rootY].val = u[x].val / u[y].val / val;
} else {
rank[rootY] += rank[rootX];
u[rootX].root = rootY;
u[rootX].val = u[y].val / u[x].val * val;
}
}
vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
for (int i=0; i<equations.size(); i++) {
string from = equations[i][0], to = equations[i][1];
double val = values[i];
if(!u.count(from)) {
u[from] = Node(from, 1);
rank[from] = 1;
}
if(!u.count(to)) {
u[to] = Node(to, 1);
rank[to] = 1;
}
unionRoot(from, to, val);
}
vector<double> res;
for (auto item: queries) {
string from = item[0], to = item[1];
if(!u.count(from) || !u.count(to) || findRoot(from) != findRoot(to)) {
// from 或 to 不存在, 或者 在两颗不同的树上(不能确定值)
res.push_back(-1);
continue;
}
res.push_back(u[from].val / u[to].val);
}
return res;
}
};
|
\547. Number of Provinces
分析:求连通分量个数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
|
// dfs计数 + 访问标记
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
int m = isConnected.size(), res = 0;
vector<bool> visited(m, false);
for (int i=0; i<m; i++) { // 按行查找 [0, m-1]
if (!visited[i]) {
res++;
dfs(isConnected, i, visited); // 一次将一个连通图中的节点对应的visited[j] 设置为 1
}
}
return res;
}
void dfs(vector<vector<int>> &isConnected, int i, vector<bool> & visited) {
for (int j=0; j<isConnected.size(); j++) {
if (!visited[j] && isConnected[i][j]) {
visited[j] = 1;
dfs(isConnected, j, visited);
}
}
}
};
class UnionFind {
private:
/**
* count: 记录连通分量的个数
* parent[i]: 记录节点i的父节点
* size[i]: 记录树i的 “重要”(即整棵树的节点数量)
*/
int count;
vector<int> parent;
vector<int> size;
public:
int getCount() {
return count;
}
UnionFind(int n) {
this->count = n;
parent = vector<int>(n, 0);
size = vector<int>(n, 0);
for (int i=0; i<n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// 将 p, q 连通
void merge(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
// 小树接在大树下面, 这样比较平衡
if (size[rootP] > size[rootQ]) {
size[rootP] += size[rootQ];
parent[rootQ] = parent[rootP];
} else {
size[rootQ] += size[rootP];
parent[rootP] = parent[rootQ];
}
this->count --;
}
// 查询x的根并做路径压缩
int find(int x) {
while (parent[x] != x) {
parent[x] = parent[parent[x]]; // 压缩路径
x = parent[x];
}
return x;
}
bool connected(int p, int q) {
return find(p) == find(q); // p 与 q的根节点相同则说明p q相互连通
}
};
class Solution {
public:
int findCircleNum(vector<vector<int>>& isConnected) {
int m = isConnected.size(), res = 0;
vector<bool> visited(m, false);
UnionFind uf = UnionFind(m);
for (int i=0; i<m; i++) { // 按行查找 [0, m-1]
for (int j=0; j<i; j++) {
if(isConnected[i][j] == 1)
uf.merge(i, j);
}
}
return uf.getCount();
}
void dfs(vector<vector<int>> &isConnected, int i, vector<bool> & visited) {
for (int j=0; j<isConnected.size(); j++) {
if (!visited[j] && isConnected[i][j]) {
visited[j] = 1;
dfs(isConnected, j, visited);
}
}
}
};
|
\684. Redundant Connection
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
|
class UnionFind {
private:
/**
* count: 记录连通分量的个数
* parent[i]: 记录节点i的父节点
* size[i]: 记录树i的 “重要”(即整棵树的节点数量)
*/
int count;
vector<int> parent;
vector<int> size;
public:
int getCount() {
return count;
}
UnionFind(int n) {
this->count = n;
parent = vector<int>(n, 0);
size = vector<int>(n, 0);
for (int i=0; i<n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// 将 p, q 连通
void merge(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
// 小树接在大树下面, 这样比较平衡
if (size[rootP] > size[rootQ]) {
size[rootP] += size[rootQ];
parent[rootQ] = parent[rootP];
} else {
size[rootQ] += size[rootP];
parent[rootP] = parent[rootQ];
}
this->count --;
}
// 查询x的根并做路径压缩
int find(int x) {
while (parent[x] != x) {
parent[x] = parent[parent[x]]; // 压缩路径
x = parent[x];
}
return x;
}
bool connected(int p, int q) {
return find(p) == find(q); // p 与 q的根节点相同则说明p q相互连通
}
};
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
UnionFind uf = UnionFind(n);
vector<int> res(2, 0);
for (int i=0; i<n; i++) {
int a = edges[i][0] - 1, b = edges[i][1] - 1;
if(!uf.connected(a, b)) {
uf.merge(a, b);
} else {
res[0] = a + 1, res[1] = b + 1;
}
}
return res;
}
};
|
\695. Max Area of Island
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
class Solution {
public:
int maxAreaOfIsland(vector<vector<int>>& grid) {
int res = 0;
for (int i=0; i<grid.size(); i++) {
for (int j=0; j<grid[0].size(); j++) {
if (grid[i][j] == 1) {
res = max(res, dfs(grid, i, j));
}
}
}
return res;
}
int dfs(vector<vector<int>> &grid, int i, int j) {
if (i<0 || i==grid.size() || j<0 || j==grid[0].size()) return 0;
if (!grid[i][j]) return 0;
grid[i][j] = 0;
return 1 + dfs(grid, i, j+1) + dfs(grid, i, j-1)
+ dfs(grid, i-1, j) + dfs(grid, i+1, j);
}
};
|
\785. Is Graph Bipartite?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
public:
bool isBipartite(vector<vector<int>>& graph) {
int n = graph.size();
vector<bool> visited(n, false);
vector<bool> color(n, false);
bool flag = false;
for (int i=0; i<n; i++) { // 对图中每个节点作为起始点遍历一次,以处理多个子连通图的情形
if(!visited[i]) {
dfs(graph, i, visited, color, flag);
}
}
return !flag;
}
void dfs(vector<vector<int>>&graph, int u, vector<bool>&visited, vector<bool>&color, bool &flag) {
if(flag) return; // 已经存在子图不是二分图了
visited[u] = true; // 标记为遍历过了
for (auto v: graph[u]) {
if(!visited[v]) {
color[v] = !color[u];
dfs(graph, v, visited, color, flag);
} else {
if (color[u] == color[v]) {
flag = true;
return;
}
}
}
}
};
|
\886. Possible Bipartition
分析:与 785题类似,不同的是需要先建立图,然后判断该图是否为二分图(dfs)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
class Solution {
public:
bool possibleBipartition(int n, vector<vector<int>>& dislikes) {
vector<bool> visited(n, false);
vector<bool> color(n, false);
vector<vector<int>>graph(n);
bool flag = false;
int m = dislikes.size();
for (int i=0; i<m; i++) {
int u = dislikes[i][0]-1, v = dislikes[i][1]-1;
graph[u].push_back(v);
graph[v].push_back(u);
}
for (int i=0; i<n; i++) {
if(!visited[i])
dfs(graph, i, visited, color, flag);
}
return !flag;
}
void dfs(vector<vector<int>>&graph, int u, vector<bool>&visited, vector<bool>&color, bool &flag) {
if(flag) return; // 已经存在子图不是二分图了
visited[u] = true; // 标记为遍历过了
for (auto v: graph[u]) {
if(!visited[v]) {
color[v] = !color[u];
dfs(graph, v, visited, color, flag);
} else {
if (color[u] == color[v]) {
flag = true;
return;
}
}
}
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
|
class UnionFind {
private:
/**
* count: 记录连通分量的个数
* parent[i]: 记录节点i的父节点
* size[i]: 记录树i的 “重要”(即整棵树的节点数量)
*/
int count;
vector<int> parent;
vector<int> size;
public:
UnionFind(int n) {
count = n;
parent = vector<int>(n, 0);
size = vector<int>(n, 0);
for (int i=0; i<n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// 将 p, q 连通
void merge(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
// 小树接在大树下面, 这样比较平衡
if (size[rootP] > size[rootQ]) {
size[rootP] += size[rootQ];
parent[rootQ] = parent[rootP];
} else {
size[rootQ] += size[rootP];
parent[rootP] = parent[rootQ];
}
count --;
}
// 查询x的根并做路径压缩
int find(int x) {
while (parent[x] != x) {
parent[x] = parent[parent[x]]; // 压缩路径
x = parent[x];
}
return x;
}
bool connected(int p, int q) {
return find(p) == find(q); // p 与 q的根节点相同则说明p q相互连通
}
};
class Solution {
public:
bool equationsPossible(vector<string>& equations) {
UnionFind uf = UnionFind(26);
for(auto s: equations) {// 构建树
if(s[1] == '=') {
int a = s[0]-'a', b = s[3] - 'a';
uf.merge(a, b);
}
}
// != 违反了现有树, 即两个节点已经是相互连通的
for(auto s: equations) {
if(s[1] == '!') {
if(uf.connected(s[0]-'a', s[3]-'a'))
return false;
}
}
return true;
}
};
|
\947. Most Stones Removed with Same Row or Column
分析:假设每个stone都有一个id = i。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
|
class UF{
public:
int count; // 连通分量个数
vector<int> parents;
vector<int> rank;
UF(int n):count(n) {
parents = vector<int>(n);
rank = vector<int>(n);
for(int i=0; i<n; i++) {
rank[i] = 1;
parents[i] = i;
}
}
int findRoot(int x) {
while (x != parents[x]) {
parents[x] = parents[parents[x]];
x = parents[x];
}
return x;
}
bool isConnected(int x, int y) {
return findRoot(x) == findRoot(y);
}
void merge(int x, int y) {
int rootX = findRoot(x);
int rootY = findRoot(y);
if(rootY == rootX) return;
if(rank[rootX] > rank[rootY]) {
rank[rootX] += rank[rootY];
parents[rootY] = rootX;
} else {
rank[rootY] += rank[rootX];
parents[rootX] = rootY;
}
count --;
}
};
class Solution {
public:
int removeStones(vector<vector<int>>& stones) {
int m = stones.size();
unordered_map<int, vector<int>> m1, m2;
for (int i=0; i<m; i++) {
m1[stones[i][0]].emplace_back(i);
m2[stones[i][1]].emplace_back(i);
}
UF uf(m);
for (int i=0; i<m; i++) {
for (int j: m1[stones[i][0]]) uf.merge(i, j);
for (int j: m2[stones[i][1]]) uf.merge(i, j);
}
// uf.count表示当前的连通分量个数, 返回的结果即为res = stones.size() - uf.count
return stones.size() - uf.count;
}
};
|
\1267. Count Servers that Communicate
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public:
int countServers(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<int> row(m, 0), col(n, 0);
int res = 0;
for(int i=0; i<m; i++) {
for(int j=0; j<n; j++) {
if(grid[i][j] == 1) {
row[i] ++;
col[j] ++;
}
}
}
for (int i=0; i<m; i++) {
for (int j=0; j<n; j++) {
if(grid[i][j]==1 && (row[i]>1 || col[j]>1)) ++res;
}
}
return res;
}
};
|
\1319. Number of Operations to Make Network Connected
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution {
public:
int makeConnected(int n, vector<vector<int>>& connections) {
if(connections.size() < n-1) return -1;
vector<vector<int>>graph(n);
vector<bool>visited(n, false);
int components = 0;
// 构建图
for (auto v : connections) {
graph[v[0]].push_back(v[1]);
graph[v[1]].push_back(v[0]);
}
for (int i=0; i<n; i++) {
if(!visited[i]){
++ components;
dfs(graph, i, visited);
}
}
return components-1;
}
void dfs(vector<vector<int>>&graph, int u, vector<bool>&visited) {
visited[u] = true;
for (auto v: graph[u]) {
if(!visited[v])
dfs(graph, v, visited);
}
}
};
|
\1361. Validate Binary Tree Nodes
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
|
class UnionFind {
private:
/**
* count: 记录连通分量的个数
* parent[i]: 记录节点i的父节点
* size[i]: 记录树i的 “重要”(即整棵树的节点数量)
*/
int count;
vector<int> parent;
vector<int> size;
public:
int getCount() {
return count;
}
UnionFind(int n) {
count = n;
parent = vector<int>(n, 0);
size = vector<int>(n, 0);
for (int i=0; i<n; i++) {
parent[i] = i;
size[i] = 1;
}
}
// 将 p, q 连通
void merge(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
// 小树接在大树下面, 这样比较平衡
if (size[rootP] > size[rootQ]) {
size[rootP] += size[rootQ];
parent[rootQ] = parent[rootP];
} else {
size[rootQ] += size[rootP];
parent[rootP] = parent[rootQ];
}
count --;
}
// 查询x的根并做路径压缩
int find(int x) {
while (parent[x] != x) {
parent[x] = parent[parent[x]]; // 压缩路径
x = parent[x];
}
return x;
}
bool connected(int p, int q) {
return find(p) == find(q); // p 与 q的根节点相同则说明p q相互连通
}
};
class Solution {
public:
bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) {
vector<int> parents(n, -1);
UnionFind uf(n);
for (int i=0; i<leftChild.size(); i++) {
if(leftChild[i] == -1) continue;
if(parents[leftChild[i]] != -1) // 已经存在一个父节点了,故 有两个父节点,该树不是合法二叉树
return false;
else {
parents[leftChild[i]] = i; // 更新leftChild[i] 的父节点
uf.merge(i, leftChild[i]); // 合并i 与 leftChild[i], 即连通
}
}
for (int i=0; i<rightChild.size(); i++) {
if(rightChild[i] == -1) continue;
if(parents[rightChild[i]] != -1)
return false;
else {
parents[rightChild[i]] = i;
uf.merge(i, rightChild[i]);
}
}
int num = 0;
for (int i=0; i<n; i++) {
if(parents[i] == -1) num++;
}
// num == 1 即只有一个根,getCount() == 1则表示只有一棵树
return num == 1 && uf.getCount() == 1;
}
};
|
\1391. Check if There is a Valid Path in a Grid
分析:将Street [1-6] 2个可能的方向(包括来源 和 去向 各两个)构成一条完整的路径,使用dir[12][2]表示, 若两个节点能够形成合法路径,则合并两个节点;其他节点类似 遍历所有节点后。最后使用Union Find算法的 isConnected(0, m*n-1)判断是否形成一条合法通路。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
|
class UF{
public:
int count; // 连通分量个数
vector<int> parents;
vector<int> rank;
UF(int n):count(n) {
parents = vector<int>(n);
rank = vector<int>(n);
for(int i=0; i<n; i++) {
rank[i] = 1;
parents[i] = i;
}
}
int findRoot(int x) {
while (x != parents[x]) {
parents[x] = parents[parents[x]];
x = parents[x];
}
return x;
}
bool isConnected(int x, int y) {
return findRoot(x) == findRoot(y);
}
void merge(int x, int y) {
int rootX = findRoot(x);
int rootY = findRoot(y);
if(rootY == rootX) return;
if(rank[rootX] > rank[rootY]) {
rank[rootX] += rank[rootY];
parents[rootY] = rootX;
} else {
rank[rootY] += rank[rootX];
parents[rootX] = rootY;
}
count --;
}
};
class Solution {
public:
bool hasValidPath(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
UF uf(m * n);
for (int i=0; i<m; i++) {
for (int j=0; j<n; j++) {
int index = grid[i][j] - 1;
// cout<<i<<" "<<j<<" "<<index<<endl;
int dir[12][2] = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}, {0, -1}, {1, 0},
{0, 1}, {1, 0}, {0, -1}, {-1, 0}, {-1, 0}, {0, 1}};
for(int k=2*index; k<=2*index+1; k++) {
int nx = i + dir[k][0], ny = j + dir[k][1];
if(!isSafe(grid, nx, ny)) continue;
int index2 = grid[nx][ny] - 1;
// cout<<nx<<" "<<ny<<" "<<index2<<endl;
for (int l=2*index2; l<=2*index2+1; l++){
int px = nx + dir[l][0], py = ny + dir[l][1];
if(!isSafe(grid, px, py)) continue;
if(px == i && py == j) {
uf.merge(i*n+j, nx*n+ny);
}
}
}
if(uf.isConnected(0, m*n-1)) return true;
}
}
return uf.isConnected(0, m*n-1);
}
bool isSafe(vector<vector<int>>&grid, int x, int y) {
return x>=0 && x<grid.size() && y>=0 && y<grid[0].size();
}
};
|
\1631. Path With Minimum Effort
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
|
// dijkstra算法
struct State {
int x, y; // 当前位置的坐标
int curEffort; // 从起始点到当前位置的最小efforts
State(int _x, int _y, int effort):x(_x), y(_y), curEffort(effort) {;}
bool operator < (const State &b) const {
return curEffort > b.curEffort; // 由于sort默认less(升序),所以重载’<’运算符(改成小顶堆)。重载运算符的操作不能用于pair类型数据的排序,只能作用于结构体或类对象。
}
};
class Solution {
public:
int minimumEffortPath(vector<vector<int>>& heights) {
int row = heights.size(), col = heights[0].size();
vector<int> efforts(row*col, INT_MAX);
vector<int> visited(row*col, 0);
efforts[0] = 0; // 从起始点到(i, j)的最小efforts
priority_queue<State> pq;
pq.emplace(0, 0, 0);
while (!pq.empty()) {
State curState = pq.top();
pq.pop();
int x = curState.x, y = curState.y, curEffort = curState.curEffort;
int pre=x*col+y;
cout << curEffort<<endl;
if(visited[pre]) continue;
visited[pre] = true;
if(x == row-1 && y == col-1) return curEffort;
efforts[pre] = curEffort;
for (auto item: adj(heights, x, y)) {
int nx = item.first, ny = item.second;
int next=nx*col+ny;
if(!visited[nx*col+ny]) {
pq.emplace(nx, ny, max(curEffort, abs(heights[nx][ny] - heights[x][y])));
}
}
}
return efforts[row*col-1];
}
vector<pair<int, int>> adj(vector<vector<int>> &matrix, int x, int y) {
int dir[4][2] = {{0,1}, {0,-1}, {-1,0}, {1,0}};
vector<pair<int, int>> neibors;
for (int i=0; i<4; i++) {
int nx = x + dir[i][0];
int ny = y + dir[i][1];
if(nx < 0 || nx >= matrix.size() || ny < 0 || ny >= matrix[0].size()) continue;
neibors.push_back({nx, ny});
}
return neibors;
}
};
// 并查集
class UnionFind {
private:
int count; // 连通分量个数
vector<int> parents;
vector<int> rank;
public:
UnionFind(int n) {
count = n;
parents = vector<int>(n);
rank = vector<int>(n);
for (int i=0; i<n; i++) {
parents[i] = i;
rank[i] = 1;
}
}
int find(int x) {
while (x != parents[x]) {
parents[x] = parents[parents[x]];
x = parents[x];
}
return x;
}
bool isConnected(int p, int q) {
return find(p) == find(q);
}
void merge(int p, int q) {
int rootP = find(p);
int rootQ = find(q);
if (rootP == rootQ) return;
if(rank[rootP] > rank[rootQ]) { // 小树接到大树下面
rank[rootP] += rank[rootQ];
parents[rootQ] = parents[rootP];
} else {
rank[rootQ] += rank[rootP];
parents[rootP] = parents[rootQ];
}
}
};
class Solution {
public:
int minimumEffortPath(vector<vector<int>>& heights) {
vector<tuple<int, int, int>> edges;
int row = heights.size(), col = heights[0].size();
for (int i=0; i<row; i++) {
for (int j=0; j<col; j++) {
int index = i*col+j;
if(i<row-1) {
edges.emplace_back(abs(heights[i+1][j] - heights[i][j]), index+col, index);
}
if(j<col-1) {
edges.emplace_back(abs(heights[i][j+1] - heights[i][j]), index+1, index);
}
}
}
std::sort(edges.begin(), edges.end());
UnionFind uf(row * col);
int res = 0;
for (auto [w, u, v]: edges) {
uf.merge(u, v);
if(uf.isConnected(0, row*col-1)) {
res = w;
break;
}
}
return res;
}
};
|
\1905. Count Sub Islands
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
public:
int countSubIslands(vector<vector<int>>& grid1, vector<vector<int>>& grid2) {
int res = 0, m = grid1.size(), n = grid1[0].size();
for (int i=0; i<m; i++) {
for (int j=0; j<n; j++) {
if(grid1[i][j] == 0 && grid2[i][j] == 1)
dfs(grid2, i, j);
}
}
for (int i=0; i<m; i++) {
for (int j=0; j<n; j++) {
if(grid2[i][j] == 1) {
res ++;
dfs(grid2, i, j);
}
}
}
return res;
}
void dfs(vector<vector<int>> &grid, int i, int j) {
if(i<0 || i==grid.size() || j<0 || j==grid[0].size()) return;
if(grid[i][j] == 0) return;
grid[i][j] = 0;
dfs(grid, i-1, j);
dfs(grid, i+1, j);
dfs(grid, i, j+1);
dfs(grid, i, j-1);
}
};
|
Hard
\765. Couples Holding Hands
分析:couple的值是连续的两个数,可以 /2 后合并到一个树中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class UF {
public:
int count;
vector<int> parents;
UF(int n) {
count = n;
parents = vector<int>(n);
for(int i=0; i<n; i++) {
parents[i] = i;
}
}
int findRoot(int x) {
while (x!=parents[x]) {
parents[x] = parents[parents[x]];
x = parents[x];
}
return x;
}
void merge(int x, int y) {
int rootX = findRoot(x);
int rootY = findRoot(y);
if(rootX == rootY) return;
parents[rootX] = rootY;
count --;
}
};
class Solution {
public:
int minSwapsCouples(vector<int>& row) {
int n = row.size() / 2;
UF uf(n);
for(int i=0; i<row.size(); i+=2) {
int x = row[i]/2, y = row[i+1]/2;
uf.merge(x, y);
}
return n - uf.count;
}
};
|
\778. Swim in Rising Water
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
|
// TLE!!!
class UF {
public:
int count;
vector<int> parents;
vector<int> rank;
UF(int n) {
count = n;
parents = vector<int>(n);
rank = vector<int>(n);
for(int i=0; i<n; i++) {
parents[i] = i;
rank[i] = 1;
}
}
int findRoot(int x) {
while (x!=parents[x]) {
parents[x] = parents[parents[x]];
x = parents[x];
}
return x;
}
void merge(int x, int y) {
int rootX = findRoot(x);
int rootY = findRoot(y);
if(rootX == rootY) return;
if(rank[rootX] > rank[rootY]) {
rank[rootX] += rank[rootY];
parents[rootY] = rootX;
} else {
rank[rootY] += rank[rootX];
parents[rootX] = rootY;
}
count --;
}
bool isConnected(int x, int y) {
return findRoot(x) == findRoot(y);
}
};
class Solution {
public:
int swimInWater(vector<vector<int>>& grid) {
int n = grid.size();
if (n==1) return 0;
int times = 0;
UF uf = UF(n * n);
while (!uf.isConnected(0, n*n-1)) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] > times) continue;
if (i < n - 1 && grid[i+1][j] <= times) uf.merge(i * n + j, i * n + n + j); // 上下两个点合并
if (j < n - 1 && grid[i][j+1] <= times) uf.merge(i * n + j, i * n + j + 1); // 左右两个点合并
}
}
times++;
}
return times - 1;
}
};
// 改进:只用一个双循环
class UF {
public:
int count;
vector<int> parents;
vector<int> rank;
UF(int n) {
count = n;
parents = vector<int>(n);
rank = vector<int>(n);
for(int i=0; i<n; i++) {
parents[i] = i;
rank[i] = 1;
}
}
int findRoot(int x) {
while (x!=parents[x]) {
parents[x] = parents[parents[x]];
x = parents[x];
}
return x;
}
void merge(int x, int y) {
int rootX = findRoot(x);
int rootY = findRoot(y);
if(rootX == rootY) return;
if(rank[rootX] > rank[rootY]) {
rank[rootX] += rank[rootY];
parents[rootY] = rootX;
} else {
rank[rootY] += rank[rootX];
parents[rootX] = rootY;
}
count --;
}
bool isConnected(int x, int y) {
return findRoot(x) == findRoot(y);
}
};
class Solution {
public:
int swimInWater(vector<vector<int>>& grid) {
int n = grid.size();
UF uf(n * n);
int mp[n*n]; // 因为grid[i][j]都是唯一的,且范围是[0, n*n-1],所以可以使用map 一一映射,将二维转换为一维。后面对time循环
for (int i=0; i<n; i++) {
for (int j=0; j<n; j++) {
mp[grid[i][j]] = i*n+j;
}
}
for (int time=0; time<n*n; time++) {
int index = mp[time];
int x = index / n, y = index % n;
int dir[4][2] = {{1,0}, {-1,0}, {0, 1}, {0, -1}};
for (auto item: dir) {
int nx = x + item[0];
int ny = y + item[1];
if(nx<0 || nx>=n || ny<0 || ny>=n || grid[nx][ny]>time) continue;
uf.merge(index, nx*n+ny); // 合并当前节点和下一个合法的节点
}
if(uf.isConnected(0, n*n-1)) return time;
}
return -1;
}
};
|
Bit Manipulation
Easy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
class Solution {
public:
int hammingWeight(uint32_t n) {
int res = 0;
for (int i=0; i<32; i++) {
if ((n & (1<<i)) != 0) res ++; //非0则表示右数起第i+1位是1
}
return res;
}
};
// 解法2: n&(n-1) 表示去掉n的最低位上的1
class Solution {
public:
int hammingWeight(uint32_t n) {
int res = 0;
while(n) {
n = (n & (n-1));
res ++;
}
return res;
}
};
|
Backtracking
Easy
Medium
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution {
public:
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int>> res;
for (int i=0; i<nums.size(); i++) {
vector<int> one_ans;
one_ans.push_back(nums[i]);
dfs(nums, res, one_ans);
one_ans.pop_back();
}
return res;
}
void dfs(vector<int>& nums, vector<vector<int>>& res,
vector<int>& ans) {
if (ans.size() == nums.size()) {
res.push_back(ans);
return;
}
for(int i=0; i<nums.size(); i++) {
if(find(ans.begin(), ans.end(), nums[i]) != ans.end()) continue;
ans.push_back(nums[i]);
dfs(nums, res, ans);
ans.pop_back();
}
}
};
|
要解决重复问题,我们只要设定一个规则,保证在填第 cnt 个数的时候重复数字只会被填入一次即可。而在本题解中,我们选择对原数组排序,保证相同的数字都相邻,然后每次填入的数一定是这个数所在重复数集合中「从左往右第一个未被填过的数字」,即如下的判断条件:
1
2
3
|
if (i>0 && nums[i] == nums[i-1] && !vis[i-1]) {
continue;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution {
public:
vector<bool> vis;
vector<vector<int>> permuteUnique(vector<int>& nums) {
vector<vector<int>> res;
vis.resize(nums.size());
sort(nums.begin(), nums.end());
vector<int> one_ans;
dfs(nums, res, one_ans, 0);
return res;
}
void dfs(vector<int>& nums, vector<vector<int>>& res,
vector<int>& ans, int cnt) {
if (cnt == nums.size() ) {
res.push_back(ans);
return;
}
for(int i=0; i<nums.size(); i++) {
if(vis[i] || (i>0 && nums[i] == nums[i-1] && !vis[i-1])) {
continue;
}
ans.push_back(nums[i]);
vis[i] = true;
dfs(nums, res, ans, cnt+1);
vis[i] = false;
ans.pop_back();
}
}
};
|
Hard
Heap
Medium
\215. Kth Largest Element in an Array
参考:https://leetcode-cn.com/problems/kth-largest-element-in-an-array/solution/shu-zu-zhong-de-di-kge-zui-da-yuan-su-by-leetcode-/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
|
// 建小根堆(只需k个元素在堆里) 时间复杂度O(nlogk). k<n时更优
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
// 利用数组前k个位置 原地建小根堆
for (int i=0; i<k; i++) {
buildHeap(nums, i);
}
for (int i=k; i<nums.size(); i++) {
if(nums[i] > nums[0]) {
// 大于 堆顶元素,则替换
swap(nums[0], nums[i]);
// 替换堆顶元素后,调整小根堆
sink(nums, 0, k);
}
}
// 最后的堆是最大的k个元素,堆顶元素是第k大的元素
return nums[0];
}
private:
bool lessThan(int n1, int n2) {
return n1 < n2;
}
// 上浮(小的数上浮),从下到上调整堆
void buildHeap(vector<int>&a, int i) {
while (i > 0 && lessThan(a[i], a[(i-1)/2])) {
swap(a[i], a[(i-1)/2]);
i = (i-1) / 2;
}
}
// 下沉 从下到上调整堆
void sink(vector<int>& a, int i, int heapSize) {
while (i * 2 + 1 < heapSize) {
int j = i * 2 + 1;
if (j+1 < heapSize && lessThan(a[j+1], a[j])) {
// 右孩子小于左孩子
j++;
}
if(lessThan(a[i], a[j])) break;
// 父节点a[i] > 孩子节点a[j]
swap(a[i], a[j]);
i = j;
}
}
};
// 建大根堆(先按照输入的数组形式建堆,然后做堆排序), 原地建堆,没有使用额外的空间。
// 时间复杂度O((n+k)logn),空间复杂度O(logn)
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int heapSize = nums.size();
buildHeap(nums, heapSize);
for(int i=nums.size()-1; i>=nums.size()-k+1; i--) {
swap(nums[0], nums[i]);
heapSize --;
maxHeapify(nums, 0, heapSize);
}
return nums[0];
}
private:
// 构建大根堆
void buildHeap(vector<int> &a, int heapSize) {
for (int i=heapSize / 2; i>=0; i--) {
maxHeapify(a, i, heapSize);
}
}
// 调整堆,保持是大根堆,从下到上调整堆
void maxHeapify(vector<int>& a, int i, int heapSize) {
int l = i*2+1, r = i*2+2, largest = i;
if (l < heapSize && a[l] > a[largest]) {
largest = l;
}
if(r < heapSize && a[r] > a[largest]) {
largest = r;
}
if(largest != i) {
swap(a[i], a[largest]);
maxHeapify(a, largest, heapSize);
}
}
};
//快排 时间复杂度O(n),证明见 《算法导论》9.2:期望为线性的选择算法; 空间复杂度O(logn)。
class Solution {
public:
int quickSelect(vector<int>& a, int l, int r, int index) {
int q = randomPartition(a, l, r);
if (q == index) {
return a[q];
} else if(q < index) {
return quickSelect(a, q + 1, r, index);
} else {
return quickSelect(a, l, q - 1, index);
}
}
inline int randomPartition(vector<int>& a, int l, int r) {
int i = rand() % (r - l + 1) + l;
swap(a[i], a[r]);
return partition(a, l, r);
}
inline int partition(vector<int>& a, int l, int r) {
int x = a[r], i = l - 1;
for (int j = l; j < r; ++j) {
if (a[j] <= x) {
swap(a[++i], a[j]);
}
}
swap(a[i + 1], a[r]);
return i + 1;
}
int findKthLargest(vector<int>& nums, int k) {
srand(time(0));
return quickSelect(nums, 0, nums.size() - 1, nums.size() - k);
}
};
|
Graph
Divide and Conquer
Easy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
class Solution {
public:
int maxSubArray(vector<int>& nums) {
return maxSubArray(nums, 0, nums.size() - 1);
}
int maxSubArray(vector<int>& nums, int l, int r) {
if (l > r) return INT_MIN;
int mid = l + (r - l) / 2;
int max_l = maxSubArray(nums, l, mid-1);
int max_r = maxSubArray(nums, mid+1, r);
int ml = 0, mr = 0;
for (int sum=0, i=mid-1; i>=l; i--) {
sum += nums[i];
ml = max(ml, sum);
}
for (int sum=0, i=mid+1; i<=r; i++) {
sum += nums[i];
mr = max(mr, sum);
}
return max(max(max_l, max_r), ml+mr+nums[mid]);
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
|
// 对出现次数最多的数记作major_num,其数量为num。 若当前出现的数是当前次数最多的那个数,则cnt++, 反之,cnt--;当cnt=0时,重置major_num。 题目保证一定存在出现次数最多的那个数。
class Solution {
public:
int majorityElement(vector<int>& nums) {
int major_num = nums[0], cnt = 1;
for (int i=1; i<nums.size(); i++) {
if (nums[i] == major_num || major_num == INT_MAX) {
cnt ++;
if (major_num == INT_MAX) major_num = nums[i];
}
else {
cnt --;
if(cnt == 0) major_num = INT_MAX;
}
}
return major_num;
}
};
class Solution {
public:
int majorityElement(vector<int>& nums) {
if (nums.size() <= 1) return nums[0];
sort(nums.begin(), nums.end()); // O(nlogn)
return nums[int((nums.size())/2)];
}
};
|
Medium
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
|
// 平均时间复杂度O(n),最差时间复杂度O(n^2),空间复杂度O(1)
class Solution {
public:
// 分治法: 排序成 elements > pivot > pivot (这里将子数组的第一个元素作为pivot)
int findKthLargest(vector<int>& nums, int k) {
int left = 0, right = nums.size()-1, kth;
while(true) {
int idx = partition(nums, left, right);
if(idx == k-1) {// 找到第k大的数
kth = nums[idx];
break;
} else if(idx > k-1) {
right = idx - 1;
} else {
left = idx + 1;
}
}
return kth;
}
int partition(vector<int>& nums, int left, int right) {
int pivot = nums[left], l = left+1, r = right;
while (l <= r) {
if (nums[l] < pivot && nums[r] > pivot){
swap(nums[l++], nums[r--]);
}
if (nums[l] >= pivot) l++;
if (nums[r] <= pivot) r--;
}
swap(nums[left], nums[r]);
return r;
}
};
//最小堆
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
multiset<int> mset;
for (int num : nums) {
mset.insert(num);
if (mset.size() > k) {
mset.erase(mset.begin());
}
}
return *mset.begin();
}
};
|
Hard