写在前面

差分隐私从开始了解也有一段时间了，是时候写下paper笔记了。由于笔者能力或理解有限，如有不当之处欢迎拍砖~ 期待能与同道中的你一同研究学习（除paper外，中文的相关学习资料不多）

本文参考《本地化差分隐私研究综述》，文中所引图片版权归属原作者，如侵权请邮件联系笔者。

Zotero-Paper联动链接–读者可忽略

本地化差分隐私的引出

如何在数据发布核分析的同时保证其中的个人敏感信息不被泄露是当前面临的重大挑战。 中心化差分隐私保护技术建立在可信第三方数据收集者的假设基础上，然而该假设在现实中不一定成立。 因此，本文作者提出 本地化差分隐私 ，其具有强隐私保护性，不仅可以抵御具有任意背景知识的攻击者，而且能够防止来自不可信第三方的隐私攻击，对敏感信息提供更全面的保护。

总结

本文主要指出了截止2018年中心化差分隐私在实际应用中的弊端，进而提出相对更贴合实际的本地化差分隐私技术，并总结了两者异同点、数据保护框架，以及本地化查分隐私方法的分析对比，对未来研究方向做分析并指出研究中的挑战性问题。个人认为能够为刚刚进入本地化差分隐私研究领域的人提供一个大致的框架以及基本概念的梳理，可进一步追溯参考文献进行研究。

引言

就隐私保护技术而言， 隐私保护程度和数据可用性是最重要的衡量指标。

为平衡隐私保护程度和数据可用性，引入形式化定义对隐私进行量化===»> 差分隐私[1-3]技术的提出。

隐私保护的强度，即 任意一条记录的添加或删除，都不会影响最终的查询结果，同时，该模型定义了极为严格的攻击模型，其不关心攻击者具有多少背景知识。 相比k-匿名[4], l-多样性[5] 和 t-紧密型[6]等需要特殊攻击假设和背景知识的方法，差分隐私因其独特的优势成为学术界的研究热点。

传统的差分隐私技术 将原始数据集中到一个数据中心，然后发布满足差分隐私的相关统计信息， 称其为中心化差分隐私（centralized differential privacy）技术。其对敏感信息的保护 始终基于 可信的第三方数据收集者 这一假设。

本地化差分隐私技术（local differential privacy）【7，8】在 不可信第三方数据收集者的场景下， 其在继承中心化隐私技术定量化定义隐私攻击的基础上，细化了对个人敏感信息的保护。具体来说，其将数据的隐私化处理过程转移到每个用户上，使得用户能够单独地处理和保护个人敏感信息，即进行更加彻底地隐私保护。

另外，本地差分隐私扩展出了新的特性，使该技术具备两大特点：

  • 充分考虑任意攻击者的背景知识，并对隐私保护程度进行量化
  • 本地化扰动数据，抵御来自不可信第三方数据收集者的隐私攻击

众包数据采集

关于众包数据采集的隐私问题，

  • 【11】指出隐私问题是众包技术发展的一大挑战
  • 【12】提出基于k-匿名的众包数据保护方法
  • 【13】提出编码扰动的方法等

上述研究并未考虑基于背景知识的攻击。 在众包数据采集问题上迫切需要一种能够充分考虑背景知识，严格定义攻击模型的隐私保护技术。

敏感图像特征提取

图像特征提取是图像处理中最初级的运算，是进行图像识别的关键。

目前围绕图像与隐私展开的研究工作

  • 【15】以医学图像为例说明了图像中蕴含的隐私问题
  • 【16】提出人脸识别过程中通过安全多方计算（SMC）进行隐私保护
  • 【17】基于云计算环境提出图像特征提取过程中基于加密的隐私保护方法等

现有方法均建立在可信的数据收集者的基础上，在图像信息高度敏感的情形下，可信第三方数据收集者的假设难以立足。

因此，敏感图像特征提取问题上迫切需要一个能够抵御不可信第三方数据收集者的隐私模型。

  • 【18】指出云计算环境下本地化差分隐私技术在图像处理这一领域的巨大潜力。

本地化差分隐私技术已成为继中心化差分隐私技术之后一种强健的隐私保护模型【9，19，20】

对于本地化差分隐私的研究和应用，主要考虑两个问题：

  • 如何设计满足ε本地化差分隐私的数据扰动算法，以保护其中的敏感信息
  • 数据收集者如何对查询结果进行求精处理，以提高统计结果的可用性

基础知识

本地化差分隐私的定义

扰动机制

随机响应（randomized response）技术 — 主流扰动机制

主要包括两个步骤：扰动统计和校正

离散型数据的随机响应

方法有PAPPOR 和 S-Hist 、k-RR 和 ORR

连续型数据的随机响应

方法有MeanEst和 Harmony-Mean等

难点主要在两个方面：

  • 如何合理设置离散化的两个数值
  • 如何保证统计结果的无偏性

本地化与中心化差分隐私的异同点

  • 组合特性

    • 差分隐私技术具有序列组合性和并行组合性两种特性[27],序列组合性强调隐私预算可以在方法的不同步骤进行分配,而并行组合性则是保证满足差分隐私的算法在其数据集的不相交子集上的隐私性.从定义上来看,中心化差分隐私定义在近邻数据集上,本地化差分隐私则是定义在其中的两条记录上,而隐私保证的形式并未发生变化,因此本地化差分隐私将上述两种组合特性继承下

  • 可信与不可信第三方

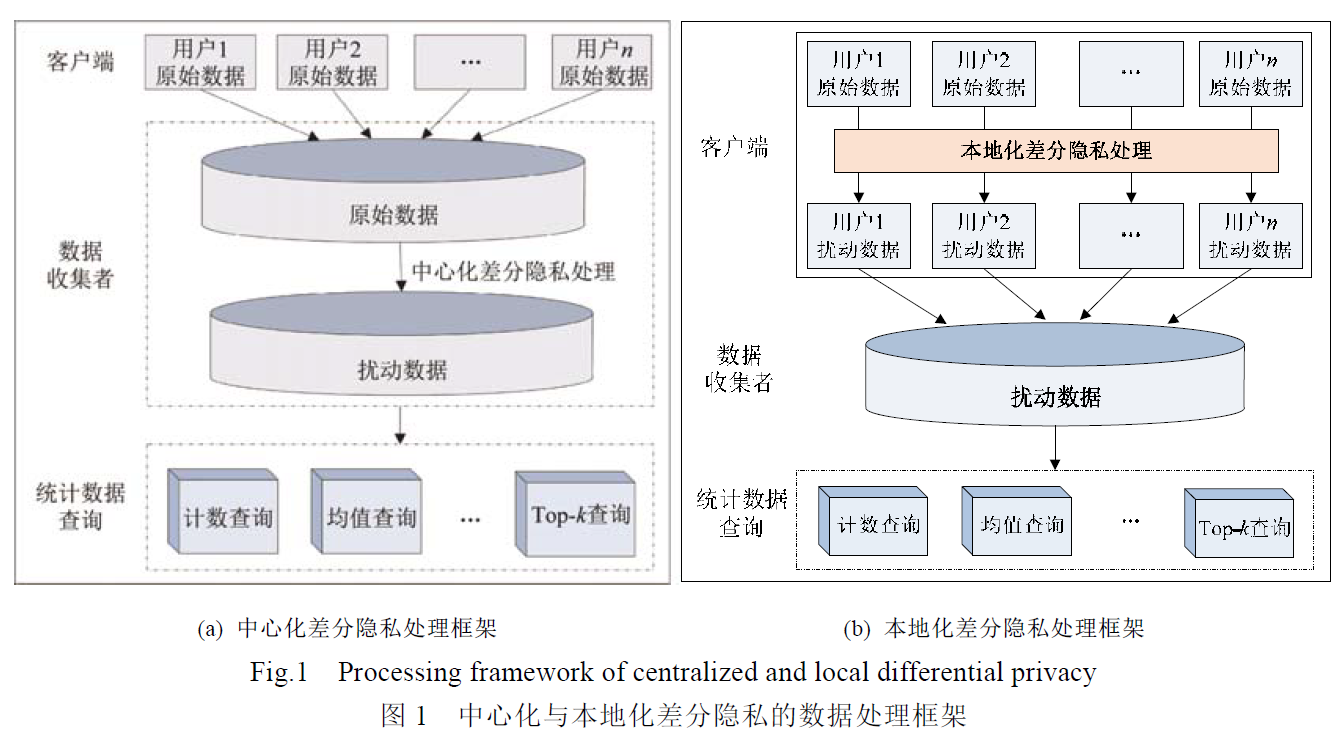
  • 噪声机制

    • 在中心化差分隐私保护技术中,为保证所设计的算法满足ε -差分隐私,需要噪声机制的介入,拉普拉斯机制[28]和指数机制[29]是其最常用的两种噪声机制,其中,拉普拉斯机制面向连续型数据的查询,而指数机制面向离散型数据的查询.上述两种噪声机制均与查询函数的**全局敏感性[28]**密切相关,而全局敏感性则是定义在至相差一条记录的近邻数据集之上,使得攻击者无法根据统计结果推测个体记录,即将个体记录隐藏在统计结果之中.在本地化差分隐私中,每个用户将各自的数据进行扰动后,再上传至数据收集者处,而任意两个用户之间并不知晓对方的数据记录,亦即,本地化差分隐私中并不存在全局敏感性的概念,因此,拉普拉斯机制和指数机制并不适用.

  • 应用场景

    • 中心化差分隐私技术通过定义全局敏感性为查询结果添加响应噪声,再以统计的方式限制隐私信息泄露的量化边界,从而能将个体记录隐藏在统计结果中.因此,中心化差分隐私技术并不对统计数据量作特别要求.不同于此,本地化差分隐私技术对个体数据进行正向和负向的扰动,最终通过聚合大量的扰动结果来抵消添加在其中的正负向噪声,从而得到有效的统计结果.然而,由于噪声的随机性,要保证统计结果的无偏性,必然需要海量的数据集来实现满足数据可用性的统计精度.

基于本地化差分隐私的数据保护框架

中心化差分隐私技术的两种数据保护框架：交互式和非交互式

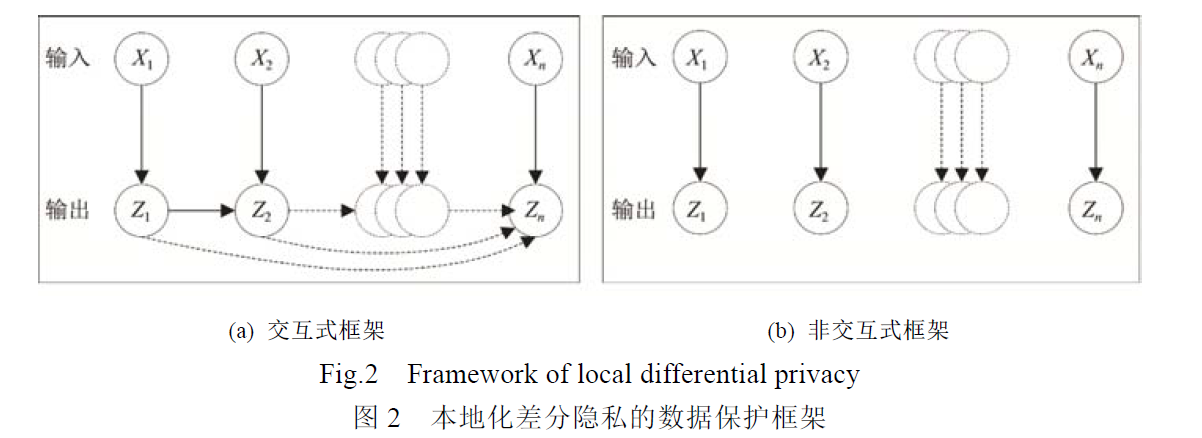
**交互式框架的第i个输出 $Z_i$ 依赖于第i个输入$X_i$ 以及前i个输出$Z_{1:i-1}$ ，但与前i个输出$X_{1:i-1}$ 无依赖关系**

非交互式框架的第i个输出 $Z_i$ 仅依赖于第i个输入$X_i$

两种数据保护框架的最大区别在于输出结果之间的关联性

  • 交互式框架适用于最终输出结果与前i个输出有依赖关系的清醒，如通过家族病史数据进行疾病诊断
  • 非交互式框架适用于前后的输入输出之间无依赖关系的情形，如商场的购物数据分析

基于本地化差分隐私的数据保护框架充分考虑了数据记录之间的相互关联关系,并以此为依据将其分为交互式和非交互式框架.而中心化差分隐私并未直接考虑数据的关联关系,

文献[40]指出数据记录中的关联性将弱化中心化差分隐私技术的保护能力,

文献[41]则进一步讨论了具有不同程度背景知识的攻击者对关联数据中的用户隐私的攻击能力,并提出基于贝叶斯理论的保护模型

主要研究方向

本地化差分隐私的扰动机制主要包括 随机响应、 信息压缩和扭曲。

随机响应技术的扰动框架简洁、直观，且其扰动程度可直接量化，因此本地化差分隐私下的研究工作大多基于随机响应技术展开，包括针对离散性数据的频数发布和针对连续型数据的均值发布。

目前（至此文收录2018年），针对本地化差分隐私的均值发布研究工作还比较少，其主要思想一般是在无偏估计的前提下对连续值进行离散化。

本地化差分隐私方法的对比与分析

基于本地化差分隐私的频数统计

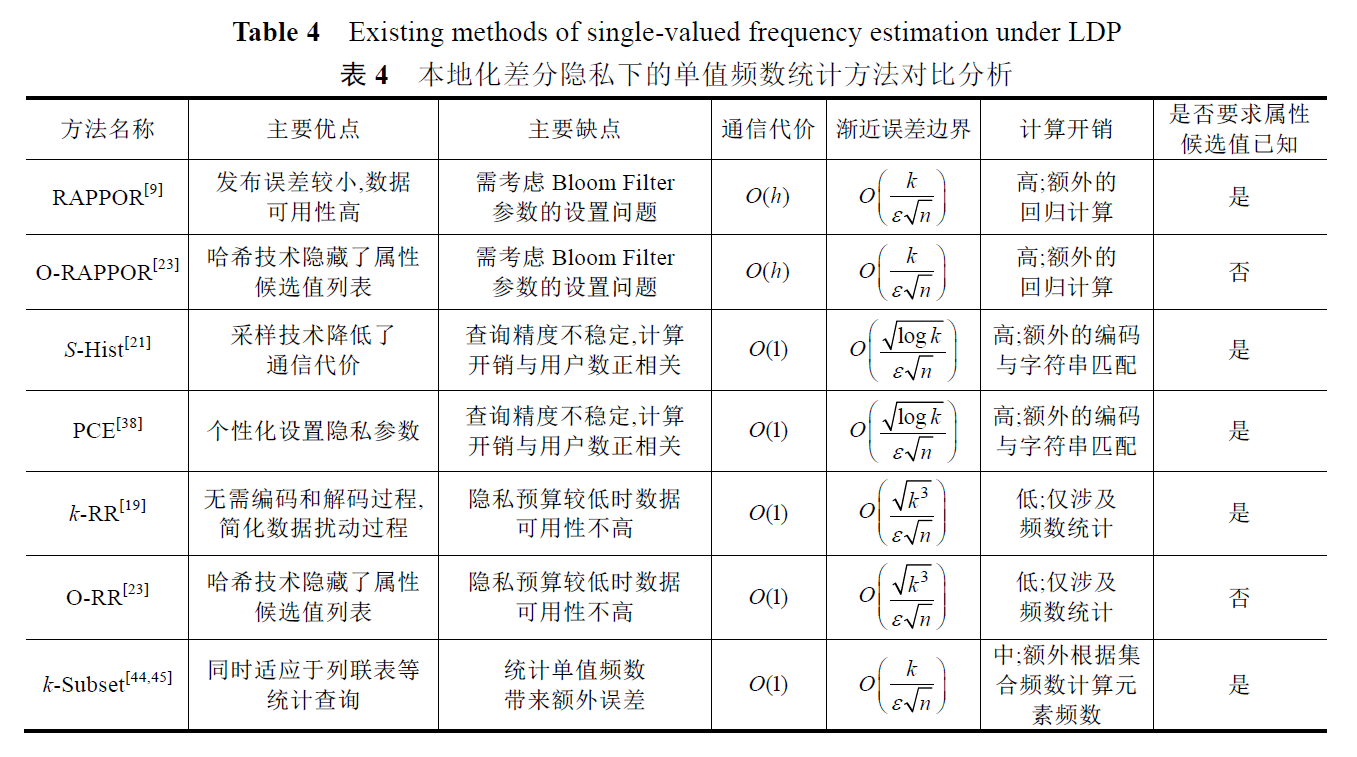
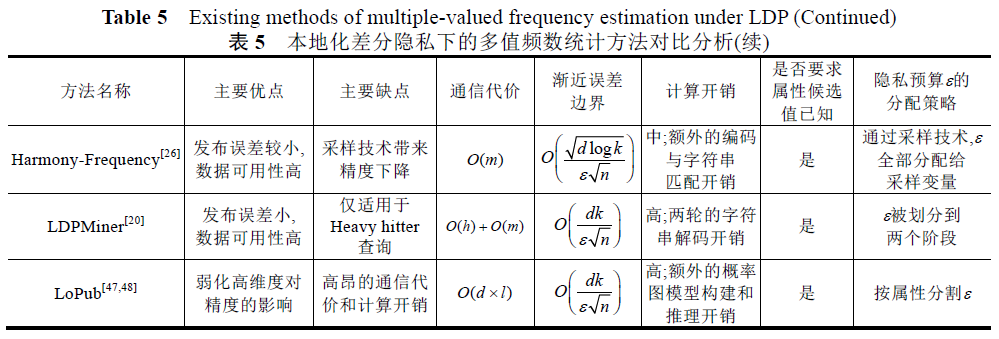
基于本地化差分隐私的均值统计

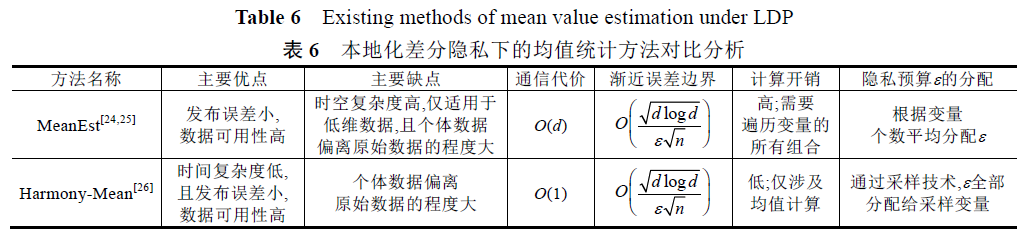
基于信息压缩和扭曲的扰动机制

未来研究挑战

现有研究

现有研究主要集中在两个方面：

  • 理论上，设计满足本地化差分隐私的保护机制
  • 方法上，对频数和均值两种统计结果进行保护

未来挑战

  • 复杂数据类型的本地化差分隐私保护

    • 目前，本地化差分隐私保护技术研究主要针对简单的数据类型，例如对包含一个或多个属性的关系数据和集值数据，进行频数统计或均值统计。然而，简单的数据类型对于当下空前的数据分析需求远远不够。（数据之间的关联性使得数据类型更复杂给隐私保护技术带来的挑战）
      • 例如 键值对，在对“键”和“值”进行隐私化处理的同时保证那个“键”和“值”的对应性
      • 图数据， 中心化差分隐私技术处理的主要难点在于图结构特点使得查询的全局敏感性极高，从而使得噪声过大。基于本地化差分隐私技术的图数据发布，不存在敏感性过大的问题，但是由于每个用户对数据的扰动过程相互独立，数据收集者如何根据扰动后的数据构建可用性高的图结构，即 如何保证原始数据之间的关联性是一大挑战 。 而且现实中很多图数据的稀疏性进一步加大了还原数据关联性的难度

  • 不同查询和分析任务的本地化差分隐私保护

    • 目前本地化差分隐私下的研究工作所针对的查询任务主要包括两类简单的聚类查询

      • 离散型数据下的计数查询
      • 连续型数据下的均值查询

    • 且数据的扰动方式一般根据查询类型而定，二者紧密耦合，使得相应扰动方式仅能支持特定的查询任务。但是面对大数据下各种复杂的查询和分析任务，只有上述两类基本的聚类查询远远不够

    • 基于本地化差分隐私保护的数据分析，目前文献【26】讨论了3中分析任务：1）线性回归；2）Logistic回归；3）SVM分类

    • 针对不同查询和分析任务的本地化差分隐私保护技术主要考虑：

      • 提供对除计数查询和均值查询以外的多种查询方式的支持；
      • 数据扰动方式与查询类型的解绑，使得扰动后的数据能够同时支持多种查询；
      • 提高数据分析结果的可用性

  • 基于本地化差分隐私的高维数据发布

    • 对于本地化差分隐私保护技术，高维数据带来了数据规模变大和信噪比降低两个方面的影响，而且还将增加通信代价。并且通信代价根据不同的扰动机制随数据维度的增加呈线性增长或指数增长，而通信代价的增加将直接为本地化差分隐私技术的应用带来限制
    • 参考文献【47-48】【20-21】采样技术降维
    • 针对此问题主要考虑：
      • 如何在一定隐私预算内衡量属性之间的关联性，从而进行降维处理
      • 如何设计推理模型，最小化边缘分布到联合分布的近似误差，提高数据可用性
      • 如何控制高维数据在用户和数据收集者之间的通信代价

参考文献

  • Video-差分隐私叶青青孙林 – 此paper一作讲解本地查分隐私，少有的中文讲座。

  • [1] Dwork C. Differential privacy. In: Proc. of the ICALP. 2006. 1–12.

  • [2] Dwork C, Lei J. Differential privacy and robust statistics. In: Proc. of the 41st Annual ACM Symp. on Theory of Computing. ACM，2009，371–380. [doi: 10.1145/1536414.1536466]

  • [7] Kasiviswanathan SP, Lee HK, Nissim K, Raskhodnikova S, Smith A. What can we learn privately. In: Proc. of the 49th Annual IEEE Symp. on Foundations of Computer Science (FOCS). IEEE, 2008. 531–540.

  • [8] Duchi JC, Jordan MI, Wainwright MJ. Local privacy and statistical minimax rates. In: Proc. of the 54th Annual IEEE Symp. on Foundations of Computer Science (FOCS). IEEE, 2013. 429–438. [doi: 10.1109/FOCS.2013.53]

  • [9] Erlingsson Ú, Pihur V, Korolova A. Rappor: Randomized aggregatable privacy-preserving ordinal response. In: Proc. of the 2014 ACM SIGSAC Conf. on Computer and Communications Security. ACM, 2014. 1054–1067. [doi: 10.1145/2660267.2660348]

  • [16] Erkin Z, Franz M, Guajardo J, Katzenbeisser S, Lagendijk I, Toft T. Privacy-Preserving face recognition. In: Proc. of the Int’l Symp. on Privacy Enhancing Technologies Symp. Berlin, Heidelberg: Springer-Verlag, 2009. 235–253.

  • [19] Warner SL. Randomized response: A survey technique for eliminating evasive answer bias. Journal of the American Statistical Association, 1965,60(309):63–69.

  • [20] Qin Z, Yang Y, Yu T, Khalil I, Xiao X, Ren K. Heavy hitter estimation over set-valued data with local differential privacy. In: Proc. of the 2016 ACM SIGSAC Conf. on Computer and Communications Security. ACM, 2016. 192–203. [doi: 10.1145/2976749.2978409]

  • [28] Dwork C, McSherry F, Nissim K, Smith A. Calibrating noise to sensitivity in private data analysis. In: Proc. of the Theory of Cryptography Conf. Berlin, Heidelberg: Springer-Verlag, 2006. 265–284.

  • [41] Yang B, Sato I, Nakagawa H. Bayesian differential privacy on correlated data. In: Proc. of the 2015 ACM SIGMOD Int’l Conf. on Management of Data. ACM, 2015. 747–762. [doi: 10.1145/2723372.2747643]